FORCED OSCILLATION DUE TO A PERIODIC EXCITATION
Consider the forced oscillation of a two-dimensional airfoil in a flow, under a harmonic exciting force. We shall have, then, the external force and moment per unit span
P = V*. Q = Q0eM (1)
where P0 and Q0 are complex constants (see § 1.8).
* The lift Цт) is defined as positive upward according to the usual sign convention in aerodynamics. The bending displacement h is positive downward. The forces on the right-hand side of Eqs. 3 are positive downward. Hence, the negative sign in front of L(r) in Eqs. 10.
Let us assume that the excitation has been operative for a long time and that the response of the system has reached a steady state.* The motion of the airfoil must be periodic and of the same period as the exciting force. Furthermore, because the system is linear, the response must be harmonic if the exciting force is. Hence, we may write
h = h0eiat, ol = а0еш (2)
where h0 and a,, are complex constants, the absolute values of which represent the amplitudes, and the arguments, the phase angles.
It is convenient to use the nondimensional time r. Then, since
![]() U
U
T~~bt
we may write
Р(Т) = РдЄІк Q(T) = Qg^
h(r) — h0eikr, а(т) = ctgetkT
where к is the reduced frequency
![]() к
к
When h(f) and а(т) are represented by Eqs. 4, the integrals involved in Eqs. 8 and 9 of § 6.8 can be evaluated. In order to avoid the mathematical difficulty of oscillatory divergence at the lower integration limit (— oo), we shall introduce a convergence factor e’T«, (e > 0), into the integrands, and pass to the limit є -> 0 through real, positive values after the integrals are evaluated. In other words, a divergent motion is considered first, but the degree of divergence is reduced to zero afterwards. The physical problem remains to be the finding of aerodynamic forces for harmonic oscillations. Let us write
lim ik f Ф(т – т0)еііт“+ет« dr0 = С(к)еікт (6)
e—й)+ J—• со
and therefore, on substituting Eq. 4,
– Tg) Ja’Oo) + ^ h"(T0) + Q — aAj a"(T0)j e"» dr0
= C(k) [ao + l – к hg + Q – ;7ca0j eikr (7)
* If the system is stable, the effect of the initial disturbance will die out as time increases. If the system is unstable, the effect of the initial disturbance will actually be magnified as time increases. Nevertheless, in both cases, the response of the system can be separated into two parts: (1) the steady-state response to the periodic force, and (2) the transient response to the initial disturbance. The first part is studied in this section.
The function C(k) is called Theodor sen’s function,* the exact expression of which, corresponding to Eq. 5 of § 6.7, is
|
Table 6.1 The Function C{k) = F – f iG, and Related Quantities
|
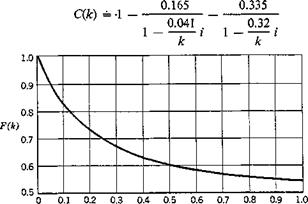
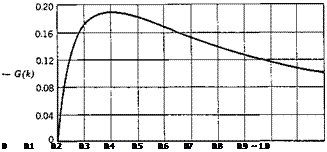
where H and К are the Hankel functions and the modified Bessel functions, respectively. The standard notations for the real and imaginary parts of C(k) are F and G, which are tabulated in Table 6.1,f and shown in Fig. 6.8.
* See §13.4.
t From Ref. 13.33. More extensive numerical tables of C(k) are given by Luke and Dengler, and Brower and Lassen, in Refs. 13.25 and 13.6, respectively.
Approximate expressions of C(k) corresponding to Eqs. 4 (R. T. Jones) and 4a (W. P. Jones) of § 6.7 are, respectively:[19]
![]() , 0.165 0.335
, 0.165 0.335
![]()
![]() C(k) = 1 –
C(k) = 1 –
1
|
|
|
Reduced frequency, k |
 |
Reduced frequency, k
Fig. 6.8. The real and imaginary parts of Theodorsen’s function Fiji) and
G(k). Note the difference in vertical scale in these two figures. F(k) tends
to 1/2 and G(k) tends to zero as к tends to infinity.
These expressions may be compared with the quasi-steady lift and moment given by Eqs. 2 and 3 of § 6.2. Specializing to harmonic oscillations, we obtain, from Eq. 2 of § 6.2,
![]()
![]()
![]() L(r)e-ikT
L(r)e-ikT
pnbU2
Comparing this with the last term of the first of Eq. 9, we see that the lift due to circulation can be obtained by multiplying the quasi-steady lift by Theodorsen’s function C(k). An investigation of the expression for the moment M shows that the resultant of the circulatory lift acts through the 1/4-chord point. The remaining terms in Eqs. 9 are of noncirculatory origin.
Let us introduce the dimensionless coefficients:
|
m ^ trpb2 |
— the mass ratio |
|
£ |
the distance of wing center of mass aft of |
|
mb |
— the elastic axis in semichords |
|
the radius of gyration (about the elastic axis) — in semichords |
The equations of motion (Eqs. 10 of § 6.8) then become, on dividing throughout the first by ітрЬ3оР and the second by ттрЬ*со2, and omitting the time factor etkr,
![]()
(ID
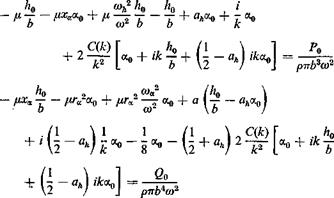 For the forced-vibration problem, the effect of the structural damping (so far neglected) must be considered, particularly in resonant conditions. The structural damping in aircraft structures is generally small. To account for the damping approximately, let us assume that the actual form of the hysteresis curve is unimportant and that the hysteresis loop can be replaced by an ellipse whose area is the same as the actual one. In other words, we assume that the effect of structural damping is revealed through the energy it dissipates per cycle. Furthermore, following Theodorsen, let us assume that the energy dissipation varies with the square of the amplitude of oscillation. Under these assumptions the effect of damping can be represented by a shift of the phase angle of the elastic restoring force. For aircraft structures the amount of this phase shift is very small, and so the structural damping may be described by a force in phase with the velocity, against the direction of motion, and of a magnitude proportional to the elastic restoring force. Thus in association with the elastic restoring force — Khh0elkr which acts against the vertical translation, there is a damping force — ighKhh0elkr. gh is called the damping coefficient. The net result is simply that the restoring force terms hKn, aKx be replaced by terms of the form hKh{ 1 + igh), a. Ka(l + iga), or, equivalently, mh coa2 be replaced by &>Ді + igh), соa2(l + iga), respectively. Cf. Appendix 3.
For the forced-vibration problem, the effect of the structural damping (so far neglected) must be considered, particularly in resonant conditions. The structural damping in aircraft structures is generally small. To account for the damping approximately, let us assume that the actual form of the hysteresis curve is unimportant and that the hysteresis loop can be replaced by an ellipse whose area is the same as the actual one. In other words, we assume that the effect of structural damping is revealed through the energy it dissipates per cycle. Furthermore, following Theodorsen, let us assume that the energy dissipation varies with the square of the amplitude of oscillation. Under these assumptions the effect of damping can be represented by a shift of the phase angle of the elastic restoring force. For aircraft structures the amount of this phase shift is very small, and so the structural damping may be described by a force in phase with the velocity, against the direction of motion, and of a magnitude proportional to the elastic restoring force. Thus in association with the elastic restoring force — Khh0elkr which acts against the vertical translation, there is a damping force — ighKhh0elkr. gh is called the damping coefficient. The net result is simply that the restoring force terms hKn, aKx be replaced by terms of the form hKh{ 1 + igh), a. Ka(l + iga), or, equivalently, mh coa2 be replaced by &>Ді + igh), соa2(l + iga), respectively. Cf. Appendix 3.
Equations 11, with the above-named modifications for the structural damping, take the form:
![]() (12)
(12)
where
The coefficients A, B, D, E are functions of со, U, gh, gx, and k. take со and к as fundamental parameters and let
The responses h0lb and cc0 depend on the magnitude and phase relations of the excitations p0, q0, the frequency со, the speed of flow U, and the wing’s geometric, elastic, and damping characteristics. Owing to the complicated expressions, the nature of the response can be best seen by examining individual examples.
Let us consider the following particular two-dimensional wing model:*
H = 76, ад =-0.15, xa = 0.25, /у* = 0.388 (20)
b — 5 inches,
<wa = 64.1 radians per second, coh — 55.9 radians per second.
Assume the wing to be excited by a periodic force acting on the elastic axis so that
P0 = const, бо = 0 (21)
It is convenient to define certain static deflection Ast corresponding to P0:
Then, according to Eqs. 16, 17, and 21,
![]() (23)
(23)
where
|£I – V(EB + F^Xf + (Ex + ga/ir[20]X) І Д| = VVTA?
The phase angle rph between the response h and the exciting force is given by the equation
tan w = ~ ^i(Er + !1ГаХ)
Дд(-£д + /<ra2X) + A j{Ej + go’ftrJ’X)
The response h leads the exciting force if iph is positive.
At a given speed of flow U, the response ratio | hjh3t | can be computed as follows: (1) Assume a value of k. From Table 6.1 find the corresponding values of F and G. (2) Calculate the coefficients AIt AB, etc., with the assumed parameters. (3) Since со = kUjb and к and U are specified, со and X — (coa/co)2 can be obtained. (4) A substitution into Eqs. 19 gives Ад and Aj. (5) Obtain the response ratio | h0/hs11 and the phase shift iph from Eqs. 23 and 24.
The results of such a calculation are shown in Fig. 6.9 where the response ratios of a wing, characterized by the dimensions and frequencies listed in Eqs. 20, at three speeds of flow U =• 7.42, 29.7, and 86.4 ft per sec, are plotted. It is seen that, as the frequency increases from zero, two peaks of response are reached, one at a frequency close to the natural frequency in bending, and the other at that close to the natural frequency in torsion. These frequencies in still air, V = 0, are 7.92 and 12.37 cycles per second respectively. Two sets of curves are presented: The solid curves are referred to an airfoil without structural damping, gh—g« — 0; and the dotted curves are referred to an airfoil with g%— g* — 0-05, a value probably high for most metal aircraft structures. It is seen that the effect of structural damping on the response is small, except near the peaks.* At zero airspeed, the resonance peaks tend to infinity at the natural frequencies of vibration if the structural damping is zero. With damping gA and ga, the peak responses vary approximately as 1 jgh and l/gx, respectively.
Such response calculations can be repeated for other speeds of flow U. A relief map of the response as a function of U and w may be plotted.
|
Fig. 6.9. Amplitude response of the vertical displacement of a wing subjected to a periodic exciting force acting on the elastic axis. |
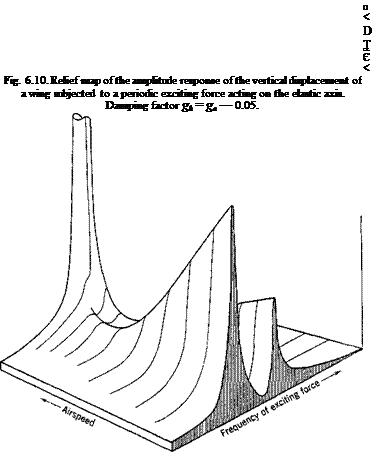 |
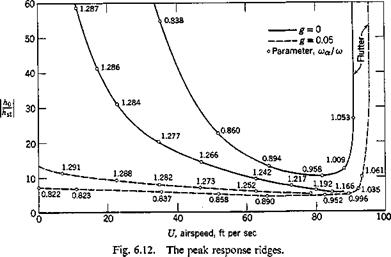
Figure 6.10 is such a relief map of the response ratio | hjhst | for the above numerical example, at g — 0.05, for which a critical flutter speed exists. The curves of Fig. 6.9 are the intersections of the relief map with particular planes perpendicular to the U axis. It is seen that, as U increases, the peak response diminishes, until, along one frequency branch, the response becomes negligibly small. Along the other frequency branch, however, a
minimum response is first reached, after which the response increases (usually rapidly) until the flutter speed is reached.
The critical flutter condition is reached when, at certain combinations of U and m, the determinant Д (Eq. 18) vanishes. Then the response ratio I h0/hst I becomes infinity. (Note that the response tends to infinity at the flutter condition, no matter whether structural damping is present or not.) The critical flutter frequency usually lies between the two natural frequencies that exist at zero airspeed.
To find the critical flutter speed and frequency, the characteristic equation
A = 0 (25)
must be solved for the pair of real variables U and со. Since A is complexvalued, both the real and imaginary parts of A must vanish. Equation 25 is actually equivalent to two real equations,
Дл — О, Д7 = 0 (26)
The solution can be obtained as follows. Let a series of values of к be assumed and the corresponding coefficients A, B, D, E calculated. By
|
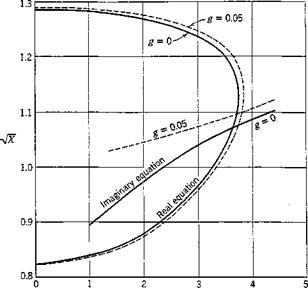
l/k Fig. 6.11. Solution of the flutter determinant. |
equating Ад and Д7 given by Eqs. 19 to zero, two quadratic equations in X are obtained. These equations can be solved for X. Since X by definition (Eq. 14) is a positive quantity, only the real positive roots have a physical meaning. Curves of Vx vs. l/k can then be plotted, such as those shown in Fig. 6.11. If the curves corresponding to Дл = 0 and A7 = 0 intersect, the points of intersection determine the values of Vx and l/k at which the determinant A vanishes. Now
Hence, the critical flutter frequency and speed are given by
If the curves Дл = 0 and Д7 = 0 do not intersect, there will be no flutter. If they intersect at more than one point, then each intersection represents a critical condition. The one having the lowest value of U is the most important. In general, it represents a transition speed below which the wing is stable and above which the wing becomes unstable. In case of doubt, however, a test of stability by the methods of §§ 6.5 and
10.6 should be made.
For the given example, Fig. 6.11 shows the existence of a critical flutter condition for gh = ga = 0, with
r =3.62, 1.072
к
Hence, the critical flutter speed is
Ua = 90.1 ft per sec and the flutter frequency is
eocr = 9.52 cycles per second
The corresponding values for gh — gx — 0.05 are
UCI = 93.0 ft per sec, cocr = 9.27 cycles per second
The main feature of the response is given by the peak values on the two ridges of the relief map (Fig. 6.10). It can be shown that, for a fixed value of the reduced frequency k, the response peaks are reached approximately where Дд vanishes. Hence, if the values of A7 are calculated for various selected points (l/к, у/Х) along Дн — 0, these values may be used to determine A. In fact,
|A| = |Arl (29)
along the Ar — 0 line. The approximate values of the response peaks can then be determined from Eq. 23, the corresponding « and U being given by Eqs. 28.
Figure 6.12 gives the peak response ridges of the example cited above. The relief map of Fig. 6.10 is constructed on the basis of Fig. 6.12.
If the exciting force is generated by a rotating eccentric weight, the
exciting force is proportional to to2; the response can be obtained from the above by appropriately multiplying the h0lhat curve by a factor to2.
Note that the coefficients of X in Eqs. 26 are nondimensional quantities, depending on the ratios ц, ah, xa, rj, and (oh/wa. Hence, the solution X is nondimensional and does not depend on the absolute values (or physical units) of the semichord b and the frequency coa. For example, if in the example specified by Eqs. 20 the semichord is changed to 2 ft, and the
|
|
frequency coa to 48 radians per second, while other quantities (ju, ah, xx, ra2, cojcoa) remain the same, then the critical reduced frequency remains the same, but the critical flutter frequency and speed become, respectively, when g — 0.05,
cocr = 43.6 radians per second, t/cr = 334 ft per sec