Form of Solution of Small-Disturbance Equations

The small-disturbance equations are (4.9,18 and 4.9,19). They are both of the form

x = Ax + Afc (6.1,1)

where x is the (А X 1) state vector, A is the (N X N) system matrix, a constant, and is the (N X 1) vector of incremental control forces and moments. In this applica­tion, the control force vector is zero, so the equation to be studied is

x = Ax (6.1,2)

Solutions of this first-order differential equation are well known. They are of the form

x(t) = x0eAr (6.1,3)

x„ is an eigenvector and A is an eigenvalue of the system. x0 is also seen to be the value of the state vector at t = 0. Substitution of (6.1,3) into (6.1,2) gives

Ax0 = Ax0

or (A — AI)x0 = 0

where I is the identity matrix. Since the scalar expansion of (6.1,5) is a system of N homogeneous equations (zeros on the right-hand side) then there is a nonzero solu­tion for x0 only when the system determinant vanishes, that is, when

det (A — AI) = 0 (6.1,6)

The determinant in (6.1,6) is the characteristic determinant of the system. When ex­panded, the result is a polynomial in A of degree N, the characteristic polynomial, and the Mh degree algebraic equation (6.1,6) is the characteristic equation of the system. Since the equation is of the Mh degree it has in general N roots A„ some real and some occurring in conjugate complex pairs. Corresponding to each real eigen­value A is a real eigenvector x0, and to each complex pair A, and A* there corresponds a conjugate complex pair of eigenvectors x0 and xjj. Since any one of the A’s can pro­vide a solution to (6.1,2) and since the equation is linear, the most general solution is a sum of all the corresponding (t) of (6.1,3), that is,

x(0 =X xo, eA” (6.1,7)

І

Each of the solutions described by (6.1,3) is called a natural mode, and the general solution (6.1,7) is a sum of all the modes. A typical variable, say w, would, according to (6.1,7) have the form

w(t) = axex" + a2eK2′ + ••• (6.1,8)

where the а і would be fixed by the initial conditions. The pair of terms corresponding to a conjugate pair of eigenvalues

A = n ± ito (6.1,9)

is аІе, мНш)’ + a2e<-n~iw)‘ (6.1,10)

Upon expanding the exponentials, (6.1,10) becomes

en,(Ax cos cot + A2 sin cot) (6.1,11)

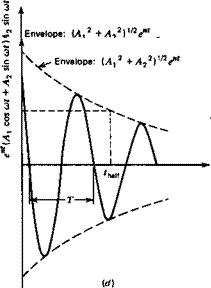
where A, = (a, + a2) and A2 = i(a] — a2) are always real. That is, (6.1,11) describes an oscillatory mode, of period T = 2ттІш, that either grows or decays, depending on the sign of n. The four kinds of mode that can occur, according to whether A is real or complex, and according to the sign of n are illustrated in Fig. 6.1. The disturbances shown in (a) and (c) increase with time, and hence these are unstable modes. It is conventional to refer to (a) as a static instability or divergence, since there is no ten­dency for the disturbance to diminish. By contrast, (c) is called dynamic instability or a divergent oscillation, since the disturbance quantity alternately increases and di­minishes, the amplitude growing with time. (b) illustrates a subsidence or conver­gence, and (d) a damped or convergent oscillation. Since in both (b) and id) the dis­turbance quantity ultimately vanishes, they represent stable modes.

It is seen that a “yes” or “no” evaluation of the stability is obtained simply from the signs of the real parts of the As. If there are no positive real parts, there is no in­stability. This information is not sufficient, however, to evaluate the handling quali-

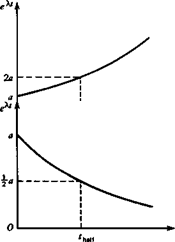Figure 6.1 Types of solution, (a) A real, positive. (b) A real, negative, (c) A complex, n > 0. (d) A complex, n < 0.

ties of an airplane (see Chap. 1). These are dependent on the quantitative as well as on the qualitative characteristics of the modes. The numerical parameters of primary interest are

277

1. Period, T = —

0)

2. Time to double or time to half.

3. Cycles to double (/Vdoub|e) or cycles to half (NhM).

The first two of these are illustrated in Fig. 6.1. When the roots are real, there is of course no period, and the only parameter is the time to double or half. These are the times that must elapse during which any disturbance quantity will double or halve it­self, respectively. When the modes are oscillatory, it is the envelope ordinate that doubles or halves. Since the envelope may be regarded as an amplitude modulation,
then we may think of the doubling or halving as applied to the variable amplitude. By noting that log,, 2 = – loge = 0.693, the reader will easily verify the following rela­tions:

Time to double or half:

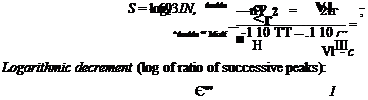Cycles to double or half:

In the preceding equations,

con = (со2 + n2)112, the “undamped” circular frequency £ = – n/co„, the damping ratio