Inverse Methods of Solution
The methods discussed here—superposition of distributed singularities (i. e., panel methods) and finite-difference solutions to the nonlinear differential equations,—are solutions to the direct problem: namely, given the airfoil shape, we find the pressure distribution. The inverse, or design, problem is the focus of much current analysis effort. Here, a streamwise velocity and/or pressure distribution along the airfoil surface is specified at the outset to meet certain performance criteria. Examples include the following:
1. A streamwise pressure distribution might be specified along the airfoil surface that would encourage the preservation of a laminar boundary layer over a considerable chordwise extent. This would result in a significant reduction in drag because the skin-friction drag due to a laminar boundary layer is much less than that due to a turbulent boundary layer.
2. A streamwise pressure distribution that would delay boundary-layer separation and hence reduce the form drag of the airfoil might be specified along the airfoil surface.
3. A streamwise pressure distribution with a relatively low suction peak on the upper surface of the airfoil might be chosen. This would result in a higher critical Mach number for the airfoil, meaning that it could operate efficiently at a higher subsonic cruise speed than an airfoil with a conventional pressure distribution. Increased speed and efficiency are important design objectives.
The required velocity or pressure distribution around the airfoil specifies an airfoil shape, which must be found. An iteration process involving variation of the airfoil shape with conformal-mapping techniques (see Section 5.2) is used in computer codes to find a configuration that is physically correct (i. e., meets the requirements that the shape is closed, with proper flow conditions at infinity). Such airfoils are said to be “tailored” because they were designed for a certain behavior specified in advance. For example, recent work at Delft University on low-drag sailplane airfoils specified a pressure distribution on the lower airfoil surface that was designed to promote laminar flow over the entire lower surface. Such airfoils yield performance close to the theoretical maximum in terms of the L/D ratio.
Motivation for many of the modern low-speed airfoil-design procedures comes from what might appear to be an unexpected source; namely, international competition soaring. The quest for improved performance from the standpoint
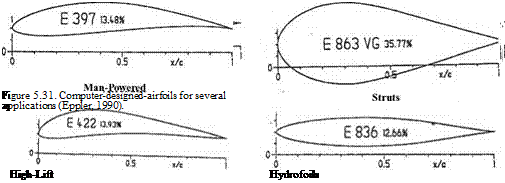 |
of reduced L/D, (see Chapter 1), has led to improvements in every facet of low – speed airplane design. One of the most important ways to achieve increases in performance is through improvements in airfoil characteristics. Much of the early work to improve low-speed airfoils was conducted by German engineering students working at the Akaflieg groups in major universities. This work continues the tradition begun in the 1920s and 1930s, starting with the development of the Jou – kowski airfoils and their derivatives, the Gottingen airfoils. Two students, Richard Eppler and Franz Wortmann at the University of Stuttgart, were responsible for leading the revolution in laminar-flow airfoil design in the last several decades. Their airfoils are now in widespread use throughout the world, and their computer codes have been adapted by many institutions, including NASA. Figure 5.31 illustrates several of Eppler’s airfoil designs for different aeronautical applications. We
examine two of the airfoil shapes shown in Fig. 5.31. The discussion follows that given in Boermans (1997).
Consider the E.361 airfoil design for a helicopter rotor shown in Fig. 5.31. When a helicopter is in forward flight, the rotating blades experience a high resultant velocity (and low Q) as they sweep forward into the oncoming stream (i. e., “advancing” blades), and a low resultant velocity (and higher Q ) as they rotate farther and then move in the streamwise direction (i. e., “retreating” blades). Compared to a similar conventional NACA airfoil, the pressure distribution on the E.361 at low Q (a = 1°) is flattened. This reduction of the suction peak at about 10 percent chord allows for a delay in the onset of compressibility effects on the advancing helicopter blades, with a resulting increase in blade performance. The E.361 also has a more gradual onset of stall and a larger Clmax compared to a conventional NACA section.
We now consider the Eppler E.476 airfoil tailored for an aerobatic aircraft application (Fig. 5.31). A desirable airfoil shape for an aerobatic aircraft is that the airfoil is symmetrical because the aircraft must have the same behavior in normal and in inverted flight. High-lift coefficients also are required for such an aircraft; the tailored airfoil has a higher Qmax than a comparable NACA symmetrical airfoil. The E.476 has a gradual stall. However, an airfoil shape may be tailored to have a sharp (i. e., hard) stall because such stall behavior is desirable in an aerobatic aircraft when abrupt maneuvers are required.
5.5 Summary
The goal of this chapter is to provide the student with a solid grounding in the physical behavior of airfoils as well as an introduction to numerical methods, which should be studied in detail in other courses covering numerical analysis. Most modern airfoils are designed by using computer codes. The codes range in complexity from simple panel codes to CFD codes for solving nonlinear-flow problems. There is considerable emphasis on the inverse-airfoil problem. The future of aeronautical engineering clearly is digital regarding analysis, design, and production. It eventually will be possible to design reliably an airfoil or a complete wing by computer, with computer “experiments” taking the place (at least partially) of the typical expensive testing with physical hardware. Major benefits include the ability to vary the parameters over wider ranges than might be attainable in wind-tunnel testing. However, at present, there still is considerable dependence on wind-tunnel testing for verifying and “tweaking” or correcting results of the computational effort.
That this procedure works is demonstrated by the outstanding results achieved by Boermans at Delft University of Technology and by other investigators. New laminar-flow airfoils were developed by computational methods and then subjected to careful testing and tuning in a low turbulence wind tunnel at Delft University. For example, a new series of airfoils was developed that have laminar flow over 96 percent of the lower surface. These improvements led to sailplanes with demonstrated glide ratios greater than 60:1. This airfoil technology also is being applied currently in Europe to a new family of high-performance commercial aircraft.
Students reading this textbook who require detailed information regarding performance and, perhaps, the actual airfoil coordinates needed to reproduce an airfoil for applications are referred to Web sites that provide data for thousands of
airfoil shapes. There also are Web sites that provide airfoil-design programs and a considerable selection of tutorial material. These items make it easy for students to supplement the material in this chapter and provide additional tools for the latter application of methods discussed herein. An interesting review of airfoil development is provided by Gregorek (1999).











