Matching of Flow Descriptions in Different Regions

To determine the unknown constants that enter the asymptotic expansions of the solutions in different parts of the flow and also the boundary conditions at the contour of the two-dimensional domain S for quasi-harmonic equation (2.22) of the channel flow, it is necessary to match these expansions in the overlap regions. From a physical viewpoint, the matching procedure is sim­ilar to accounting for the interaction of different parts of the flow. From a mathematical viewpoint the process of asymptotic matching allows attaining uniqueness of the composite uniformly valid solution of the problem.

We match of the flow characteristics in the different regions in accor­dance with the scheme shown in Fig. 2.2, where for simplicity the sequence of matching is shown in a two-dimensional case.

• In the first stage, match the velocity potential (pu of the upper flow with the potential (fe of the flow near the leading (side) edge hfa)- This step will result in the determination of parameters аі, а2,аз, а4, and du.

• In the second stage, match the channel flow potential p with potential (fe

of the flow near the leading (side) edge This step gives the possibility

of determining the boundary condition for the channel flow quasi-harmonic equation at contour /1, as well as the magnitudes of d and the strength Q of the contour distribution of sources (sinks) in expression (2.31).

• In the third stage, match the upper flow potential tpu with the trailing edge flow potential (fte – This step will determine parameters 61,6^, 63”, and eu. Imposing the Kutta-Zhukovsky condition in the form of equation (2.5), find the relationship of parameters 6^,63 with parameters b^b^.

• Finally, in the fourth step, match the pressure coefficient in the flow below the trailing edge pe with the channel flow pressure coeffcient p.

In what follows, we use the “asymptotic matching principle,” as introduced by Van-Dyke [38], namely: the “ m-term inner expansion of the n-term outer expansion is equal to the n-term outer expansion of the m-term inner ex­pansion,” where m and n are integers. Note that within the formalism of the method of matched expansions, the term “outer” expansion stands for the asymptotic expansion, obtained in variables, based on the primary charac­teristic lengths of the problem. The “inner ” expansion implies the use of variables stretched with the help of the gauge function of a small parameter so that they have the order of 0(1) in the regions of the nonuniform validity of the outer expansion.

To match in the first stage, it is necessary to derive an asymptotic representation of the upper flow potential pu at points of a normal v in the immediate vicinity of the leading (side) edge. This asymptotic expansion has been obtained previously and is given by expressions (2.25) and (2.32). Replacing the variable v in (2.32) by h*eD, we obtain the following two-term asymptotic expansion:

7Г 7Г

where /г*е, as earlier, is the instantaneous distance of the edge vertex from the ground, which has the order of O(/i0), and (asw) = au(M) — ag(Z,£) is the difference between the downwash upon the upper surface of the wing and that upon the ground in the vicinity of the leading edge. The first term of expression (2.62) is known from the theory of potential functions to reflect the behavior of a potential near a line distribution of sources. Other terms describe the behavior of the surface distribution of sources (simple layer) near the edge. Parameters A(l, t) and A2(l, t) characterize the influence of distant sources. Expressions A and A2 are cumbersome in the general case, so they are not presented here, but will be written for some concrete problems later on.

On the other hand, collecting expressions (2.39), (2.46), and (2.54), we obtain the following asymptotic expansion of the leading edge flow potential far from the edge on the upper surface of the wing (у = 1 + 0):

(file -»ipeu ~ ^ In nv + ——:£(ln тгі> — 1) + h^asi) + /г0а4, (2.63)

7Г 7Г

where h*e = h*e/h0. Equating expressions (2.62) and (2.63) in the same vari­able (u or z/), we obtain

ai = – Q(l, t), a2 = 1, (2.64)

= Ы)К = [au(l, t) – ag(Z, *)]Л*е, (2.65)

a3 = – [ЛІИх + du (l – In ) 1 – (2-66)

a4 = -(a2 – ailn -Л – Y (2.67)

7Г V rtofi’e 7

Note that after the first stage of matching, the quantity Q has been expressed through a coefficient ai, which will be determined later.

1 aS ~TZ—– hU4^o* (2.68)

In the second stage of matching, it is necessary to rewrite expression (2.39) for the leading edge flow potential in terms of the coordinate v — h*eu and pass over to the limit h0(h*e) —> 0 for у = 1 — 0 and fixed v. Taking into account (2.39),(2.47), and (2.56), on the lower surface of the wing,

This asymptotic representation should be equated to expression (2.11) for the channel flow potential щ evaluated for v — h*ev —> 0, that is,

4> ~ 4> = <Ph + 4>2ho In T – + Щ3h0

h0

Setting г/ to zero, we can determine parameters ai, a2, and d:

ai = = hie~^-> at v = «.2 = 1, (2.70)

d = Kat г/ = °; (2.71)

and also the boundary condition for the quasi-harmonic equation (2.22) on the line l which corresponds to the leading (side) edge. It follows from (2.69) at v = 0 that

(f* — on lu (2.72)

or taking into account the expressions found for a and a4, as well as for the asymptotics of the function ip*,

The boundary conditions written above must be fulfilled on the line /1, which corresponds to the leading (side) edge. Note that one of the results of match­ing in the second stage is the determination of the strength Q(l, t) of the sources distributed along the lines l and Z3. This parameter enters the ex­pression for the upper flow potential (pu. As follows from (2.70), the strength of the sources Q is proportional to the velocity of flow escaping from the chan­nel into the upper flow region. Simultaneously, it follows from comparison of expressions (2.57) and (2.70) that the strength of the square root singularity of the perturbed velocity at the leading (side) edge of the wing is directly related to the intensity of the circulatory flow around the edge.

We turn to the third stage of matching. The asymptotic representation of the upper flow potential tpu near the trailing edge can be written similarly to (2.62) as

<Pu -> <fute ~ hlDln(h0hlv) + t&Biiht) h*j> + ^B2(l, t), (2.77)

7Г 7Г 7Г

where (duw) = au(Z, t) — dWl(Z, t) is the jump discontinuity of the downwash upon the upper surface of the wing and the wake in the vicinity of the trailing edge; jE? i(/,£) and B2(l, t) are known parameters, which have the same sense as Ai(l, t) and A2(l, t). On the other hand, in the expression for trailing edge flow velocity potential ipte pass to the variable v — h0hleD and set h0 (/г*е) to zero for fixed v and у — 1+0. Accounting for (2.54) with du replaced by eu,

Equating expressions (2.77) and (2.78) in the same variable (v or z>), we obtain parameters eu, , and 63 :

b — 1, eu — (ocuw)hj. e — [qu(/,£) aWl(l, t)]htl

6+ = [в, + (l In t – )1, 7Г L h*te h0h*te )	(2.80)
b+-?± °з — _ • 7Г	(2.81)

One has to remember that h*e = h0h*e is an instantaneous distance of the trailing edge from the ground and parameters b2 and 53, entering solution

(2.58) , take different magnitudes above and below the wing (b^b^, b^b^).

To determine the relationship between b^b^ and 63 ,63 , it is necessary to impose the Kutta-Zhukovsky at the trailing edge in the form (2.5), which complies with the requirement for the continuity of pressure and normal velocity across the wake in the immediate vicinity of the trailing edge. We will show how to ensure realization of this condition for a thin edge (eu = e = e), and then results will be presented for the trailing edge with finite vertex angle.

The expression for pressure coefficient in the adopted moving coordinate system x, y, z can be calculated with the asymptotic error of the order of О(h%) as

We introduce the local coordinate system vyl, where v is the external normal to the planform contour, axis у passes through a given point of this contour and is directed upwards, and l is a local tangent to the same contour. Tangent l and normal v lie in the same plane, coinciding with the projection of the wing upon an unperturbed position of the ground. For the points of the trailing edge, follow the relationship between directional derivatives:

d, X 9 . , x 9

-=ax(v, x)-+m(v, X)Jv

в ■ , , 9 , ,«

It can be shown that in the case of an infinitely thin trailing edge, the po­tential cpte in the immediate vicinity of the edge (p —> 0) has the form

<Pte ~ b2h%v d – + 0(^o^3/^2)> (2.83)

where above the edge b2 = b%, bs = bj, and below the edge b2 = b^, b3 = b% . Taking into account that at v = 0,

__ u h20 d<pte _ u db3 d<pte _ u db3 dv 2 h*e ’ dl 0 дГ dt 0 dt ‘

and equating for v = 0 the pressure coefficients above and below the edge (p+ = p-), we obtain the following relationship between the upper and lower values of parameters b2 and

СОЧІ lJ ті

Mi =—М2 = sin(u, x)U(t). (2.86)

Піе

In the fourth stage of matching, we take into account that far from an infinitely thin trailing edge under the wing (z> = ^/^*е ~°°іУ — 1 — 0)?

the edge flow potential (pte has the form

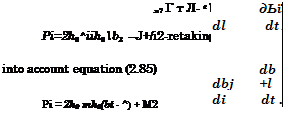Using formula (2.87) and expression (2.82) for the pressure coefficient, it is not difficult to obtain the following boundary condition for quasi-harmonic equation (2.22) on the line l2, corresponding to an infinitely thin trailing edge:

Noting that for an infinitely thin trailing edge, parameter e = eu is given by formula (2.79) and parameters b2 and 63" are expressed by (2.80) and (2.81), we finally obtain

where the relationship between the channel flow pressure coefficient p and the potential (p is given by formula (2.82). Representing the pressure in the form of an asymptotic expansion

corresponding to the adopted asymptotic expansion of the potential (/?*, we obtain the following boundary conditions for magnitudes px, p2, and p3 on the line l2:

Ph — 0, (i, z) E 12; (2.92)

(v)€,2. (2.93)

7Г 2 ’ _ / 7Г dB2 dB2- Різ = Z 7Г — (quw) In h* rite )+^-df dt.

dz dz 9<Ph 9lPh 1

dx 4 ‘ dt dx dx dz dz. In a simpler case of a wing with a straight trailing edge we obtain from expression (2.90)

The relationship between the functions рг, p2, and p3 and the corresponding terms of the asymptotic expansion of the channel flow potential is obvious:

dB2

dt

Suppose that the trailing edge has a finite vertex angle (au ^ ai, eu ф ei). Then, as a result of transfer of the boundary conditions in the local region Dte onto the line у = 1 ± 0, the corresponding expression for the velocity reveals a logarithmic singularity at the edge vertex. In principle, it is possible to correct this deficiency of the local solution and fulfill the requirement of the finiteness of the velocity at the trailing edge by introducing an additional asymptotic expansion in the vicinity of the vertex of the order O[exp(-l//i0)]. However, some analysis shows that disregard of this nonuniformity does not bring along any noticeable errors either in pressures or in integral lifting characteristics.

For the trailing edge with a nonzero vertex angle, the matching procedures result in the following expression for the pressure coefficient on the line l2:

Рі = 2[МіЦб+-^)+М2Д0^-Л0^_], (x, z)£l2, (2.99)

where parameter e was found in the form

or, finally, taking into account (2.80), (2.81), and (2.100),

dB2 dBo і

+P2-^———- gjr}, (x, z)el2. (2.101)

Thus, the application of the method of matched asymptotic expansions for treating the problem of the flow past a lifting system in close proximity of the ground leads to the following algorithmic solution with an asymptotic error of the order of 0(h„):

1. The channel flow potential щ is found through solution of quasi-harmonic equation (2.22) in the two-dimensional region S’, bounded by the wing’s planform contour with boundary conditions (2.73) at the leading edge (line l) and (2.98) or (2.101) at the trailing edge (line I2).

2. The potential tpu of the upper flow is constructed in a straightforward manner with the help of the surface distribution of the sources on the two-dimensional domain S + W + G with the addition of the admissible contour distribution of the sources along the projections of the leading (side) and trailing edges onto the plane у — 0. The strength of surface distribution of sources is equal to (—2au) upon S, (—2ag) upon G, and (—2aWl) upon W and is determined by using formulas (2.23), (2.24), and (2.27). The strengths of the sources distributed along the contour l + /3 are determined by formula (2.70).

3. Local flow solutions are constructed near the edges, depending upon the geometry and particulars of the physical performance of the latter. For example, expressions for the velocity potentials near a leading (side) and trailing edges are given by expressions (2.39) and (2.58).