Representing Static Airfoil Characteristics

The details of the airfoil pressure distribution and the variation with Mach number are important for airfoil design and airfoil selection purposes. However, in helicopter rotor performance and airloads analysis the details of the pressure distributions are usually not required because these are too expensive and time consuming to compute on a routine basis. More often it is required to mathematically model the airfoil characteristics in terms of lift, pitching moment and drag coefficients as functions of AoA. These models can then be incorporated into a blade element model, such as the approach introduced in Chapter 3, and in the “comprehensive” rotor models discussed in Section 14.11. Computational tools have not yet evolved to the point where the nonlinear performance of the airfoil at high angles of attack near stall and at high subsonic and transonic Mach numbers near drag divergence can be obtained with confidence. Therefore, reliance is placed on experimental measurements. These experimental measurements of the airfoil characteristics are usually obtained at discrete values of AoA from measurements in 2-D wind tunnel tests.

7.11.1 Linear Aerodynamic Models

In the low AoA regime, and at subsonic Mach numbers, the airloads can be ade­quately modeled using the equations

Cfi Ci — Co З- coc,

Cm = mo + ma,

Cd = do + da + d2oc2,
where со, c, mo, m, do, d, and <f2 are empirically derived coefficients obtained through curve fitting to the airfoil measurements. It is very important to recognize that these poly­nomials can only be used to represent airfoil characteristics below stall; they are totally invalid with significant amounts of flow separation or in the stalled flow regime.

The aerodynamic significance of the constants cq, c, то, m i, do, d, and <i2 are not always recognized but can be readily established. Usually it is desirable to express the airloads in terms of well-known (measurable) aerodynamic parameters, such as lift-curve-slope and zero lift angle. The usual way of representing the lift is by using the equation

where Cia is the lift-curve-slope and ao is the zero lift AoA. Expanding gives Ci = Ciaa — Ciaa о = c0 + Ca.

Therefore, со = — Ciaao and c = C/a. The pitching moment about the 1/4-chord is represented by

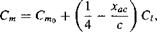(7.93)

where Cmo is the zero lift moment and xac is the position of the aerodynamic center from the leading edge. Substituting for С/ and expanding gives

which is in the form of

Cm = m0 + ma.

Therefore, the coefficient mo includes a combination of the usual aerodynamic parameters Cmo, Qa, as well as xac. The coefficient mi is a term that represents the offset of the aerodynamic center from the 1 /4-chord axis. The pressure drag can be obtained by resolving the components of the normal force and chord force through the AoA using

Cdp = Cn sin a — Ca cos or.

The total drag (profile drag) is obtained by adding the contribution from viscous shear to the pressure drag. (This is roughly C^0 at low angles of attack.) Therefore, the total drag can be written as

Typically, Tja is close to but less than one. Thus, the pressure drag becomes Cd = Q0 + Cn sin о: — r]aCn tan of cosof

— Cdo “t” Cn (1 Tjf) sin Of.

For small angles, sin a ~ a and Cn ~ С/ = C/a (a — «о) so that the total drag is

Cd = Cdо + Cia( 1 – r)a)(ot – af)a

= Cdt + CtJ – I)a)a2 – Cta( 1 – 0

= Q, – (C,.(l – i)„)c«o)a + (C,„(l – r, a)W, (7.100)

which is of the form

Cd — do’A – da + dia2. (7.101)

This equation, like the previous equations for the lift and moment, is valid only in the regimes where the flow is fully attached. Note that d = 0 for a symmetric airfoil («о = 0).