Technologies to improve cruise performance

To estimate influences on cruise performance, at first we will estimate the most important phys­ics of constant cruise. This is, for a real aircraft, some kind of oversimplification, because it omits the important segments of take-off. climb, acceleration and reserves for goaround and divert as well as the minor parts for descend, landing and taxi. But for a long range aircraft it remains the most important segment.

Constant cruise is governed by the two equilibriums of lift (L) and weight (W), and of thrust (T) and drag (D):

T = D	(37)

Thrust is paid by fuel (F)

(SFC: specific fuel consumption, see cq. (31); t: time) which reduces mass (m) or weight dF* – dm. W« m g (39) but provides range (r) via speed (v) dr a v • dt (40) When introducing the other equations in (38), simple algebraic operations provide the differen­tial Breguet-equation

T SFC – dF/dt
(38)
L V D dm
dr	(41)
SFC g m
or with engine efficiency r£ and calorific value of fuel H instead of specific fuel consumption SFC (eq. (31) >
dm m
dr ■
(42)
Simple integration gives Breguet’s range formula
L D
r	(43)

or

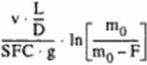(44)

Aerodynamics determine aerodynamic performance UD and so influence needed fuel F, but also provide requirements for structural layout and systems as well. Fuel, structures, engines, equipment and payload arc mass m0. Engines contribute to mass and provide its effi­ciency. which influences needed fuel. F and mass for fuel storage. The selected cruise speed

v or cruise Mach Af influences achievable L/D, engine efficiency Як or SFC, needed fuel F, and structure and equipment mass.

So. the Brcguctequation allows simple estimation of range, but it is still difficult to esti­mate improvements by singular technologies. But the Brcguctequation provides a rough estima­tion of range improvements, when only one parameter is changed, c. g. range improvement Дг provided by a pure aerodynamic improvement AL/D for the same aircraft (Яе[6] m©. F)- Now equation (43) gives

For fixed range, we can try to estimate the influences on fuel needed. (F). by the inverse Brcguct – equahon

But caution, now both m0 and F usually become strongly dependent on AL/D or ДЯе because better drag or engine cflicicnc) reduces fuel consumption F. and this reduces gross weight in*,. Therefore the inverse Brcguctequation usually calculates an aircraft whose perform­ance is not exploited To exploit performance, the aircraft has to be resided. This cannot be cal­culated by a simple equation. As a first, very rough estimation, the unresized improvement for fuel consumption, calculated by the inverse Breguet-equation (46). has to be multiplied by the factor

1 ♦ (weight part under consideration) / m„ (47)

e. g for improvement of Яе‘ (I * F/m0). But remember. The Brcguctequation only cal­culates idealised cruise flight. Therefore it may only be used for estimation of tendencies in long range flight.

Small improvements in fuel consumption by individual technologies may be compared by the percentage of the individual improvement, multiplied by

weight part influenced by thie technology / payload. (48)

This is explained in Figure 12 by several examples for an Airbus A340-300B with an assumed 15** pure drag improvement or a 159 structure weight reduction; for all examples the maximum take-ofT weight (MTOW) was maintained by adding fuel or payload.

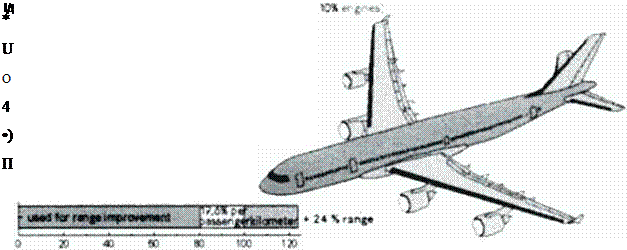figure 12 Improvement estimation