THIN-AIRFOIL PROBLEM
Consider the two-dimensional airfoil problem as a special case of the three-dimensional wing problem of Chapter 4. The dependent variables are now functions of x and z and both the upper and lower airfoil surfaces are given by
f(x, z) = z-tj(x) = 0 -?£x£? (7.1)
Note that the origin is at midchord and that the airfoil chord is c (Fig. 7.1). This choice of the origin is made for convenience in the evaluation of the Cauchy principal value integrals that will appear in the example problems.
The perturbation velocity potential Ф is defined in Section 4.2 by
Ф* = Ф + Ф„ (7.2)
where
Фоо = Uv, x + Wxz = xQ„ cos a + zQm sin a (7.3)
The exact airfoil boundary condition is the two-dimensional version of Eq. (4.12):
![]() dn/дФ „ ЭФ л.
dn/дФ „ ЭФ л.
— (-т – + 6» cos a + — + sin a = 0 on z = n
ax dx / dz
with f/oc = Q, cos or and W„ = Qx sin a. The small-disturbance approximations and limitations on the geometry introduced in Chapter 4 apply and it is assumed that the order of magnitude of the airfoil thickness ratio, camber ratio, and angle of attack can all be represented by the small parameter €.
Let us consider the following expansion for the perturbation velocity potential,
Ф = Фі + Ф2 + Фз + • ■ • (7.5)
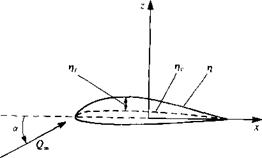 FIGURE 7.1
FIGURE 7.1
Coordinate system for airfoil problem.
Ф, = 0(еі) / = 1,2,3,… (7.6)
and the order symbol O(e) is defined by
g(e) = 0(e) as e—»0 if lim-—-<» (7.7)
e—о є
In this chapter we will carry the analysis through to second order to illustrate the method. Terms to 0(e2) will be kept and therefore the components of the free stream flow are written as
t/»=G«cosa = Q„[l-y+0(a4)] (7.8e)
Ж»= 6» sin a = Qx[a + 0(ar3)] (7.8b)
The boundary condition will be transferred to the chord line as in Eq. (4.16) and the complete boundary condition with the above substitutions becomes
dn Г ЭФ, , 1 ЭФ,
“ ~dx LG”+~aT(JC’0±)J+ Q°°a +~эГ0±)
+ n^1(JC.0±) + ^?(-t, °±) = ° (7.9)
where the ± refers to the upper and lower surfaces. For this equation to be valid for all values of the perturbation parameter e, the terms of the same order (e, є2) must individually be zero. To show this, divide the equation by є and take the limit as є goes to zero. Then all of the terms of O(e) must be zero. Now, subtract these terms from the original equation and repeat the process. This shows that all of the terms of 0(e2) must be zero.
The boundary conditions for the first – and second-order problems then become
|
0(€): |
ЭФ, dn -^(x, 0±) = Q„-l-Q„a dz dx |
(7.10) |
|
0(e2): |
ЭФ-, dn ЭФ, Э2Ф, а>0±>*Лг>0±)-’’Э2>’0±) |
(7.11) |
If Laplace’s equation for Ф, is used in the second-order condition, it becomes
At this point it is noted that the first-order boundary condition is the one that was used in the thin-airfoil treatment in Chapter 5. Now let us separate the problems at each order into a nonlifting (symmetric or thickness) problem and a lifting (camber and angle of attack) problem and introduce the camber and
ri = r}c±V,
![]() Ф] = Фі/. + Фіг Ф2 = Фгх. + Фгт
Ф] = Фі/. + Фіг Ф2 = Фгх. + Фгт
Note that the lifting potentials (Ф^, Ф2L) are antisymmetric in z and the nonlifting potentials (Фіг, Ф2г) are symmetric in z. Consequently, the z component of velocity w is continuous across the chord for the lifting problems and discontinuous for the nonlifting problems.
With the above definitions, Eqs. (7.10-7.12) become
![]()
![]()
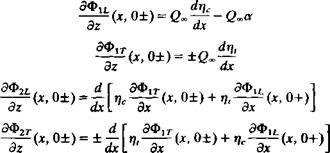 (7.15)
(7.15)
(7.16)
The complete mathematical problems that accompany the above boundary conditions (Eqs. (7.14a, ft), (7.15) and (7.16)) include Laplace’s equation for each velocity potential and a velocity field that decays to zero at infinity. A Kutta condition must be applied in the lifting problems and the nonlifting problems have zero circulation.
The solutions to the above mathematical problems can be obtained with the use of the theory of singular integral equations (see Newman,71 Section 5.7). The first-order tangential velocity component is
![]()
 |
(7.17)
(7.18)
for the lifting problem. A source distribution for Ф1г also leads to Eq. (7.17) (see Eq. 5.15). A vortex distribution solution for Ф1£. leads to an integral equation for у (Eq. 5.39) and the solution to this integral equation is given in Eq. (7.18) where y = 2u1L.
The nonunique solution (of Eq. (5.39)) with arbitrary circulation is given because for another application the solution with zero circulation will be needed. If the Kutta condition is applied, then uu,(c/2) = 0, and using (Eq.
+ (719)
The x component of velocity on the airfoil is then given by и = + uir ± uu
and the z component is obtained from the boundary conditions (Eq. (7.14a, b)).













