A Uniformly Valid Flow Description and Aerodynamic Coefficients

Uniformly valid asymptotic expansions for the velocity potentials on the upper and lower surfaces of the wing can be determined by using the rule of additive composition (see Van-Dyke [38]) in the form

P+ = ¥>U + (<p? e – ^+eu) + (*>£ – <fteu); (2-102)

<P~ =<P 1 + – v>e) + (<?te – ¥4ei)> (2.103)

where (/’u. We^te.^u^teu.^leP^tel and ‘Pi are Siven> correspondingly, by formulas (2.25), (2.39), (2.58), (2.63), (2.78), (2.68), (2.87), and (2.11).

The aerodynamic coefficients of lift Gy, longitudinal moment mz (around a point with abscissa x0), and lateral moment mx can be calculated by using the formulas

Cy = ±JJs(p–p+)ds = ^JJjjp- – p+) dS, (2.104)

mz = і jj{p–v+){x-x0)dS=^ Jjs(p–p+)(x-x0)dS, (2.105)

m* = i JJJP~ ~P+)zdS = p j jiP~ ~P+)zdS, (2.106)

where S is the reference area of the wing related to its root chord squared; Л and l are the aspect ratio and relative span of the wing; and p~ and are

uniformly valid asymptotic expressions for pressure coefficients on the lower and upper surfaces of the wing, determined by the formulas

where <p~ and (p+ are uniformly valid asymptotic representations of the ve­locity potential on the lower and upper surfaces of the wing, determined with help of formulas (2.102) and (2.103). Analyzing expressions for pressure, it is easy to see that for the upper surface of the wing, the corresponding formula is linearized, whereas for the lower surface a nonlinear formula is used. These representations of pressure are compatible with primary assumptions and asymptotics obtained for the flow velocity potentials. In fact, for small geo­metric and kinematic perturbations the flow above the wing is only slightly perturbed. On the other hand, in the flow beneath the wing, induced pertur­bations can no longer be considered small.

To evaluate the lift-to-drag ratio (aerodynamic fineness) of lifting systems in the ground effect, it is necessary to calculate part of the drag due to normal loads. At the same time, one has to take into account the fact that due to low pressure at the wing’s leading edge, the so-called suction force may occur, directed upstream and reducing the drag.

The induced drag of the wing incorporating the suction force can be determined by investigating the flow far downstream in the Trefftz plane. The induced drag coefficient is given by the formula

where /^(z), aWoo are the spanwise distributions of circulation and downwash in the Trefftz plane, whereas S is the wing’s reference area related to the square of the root chord.

To the leading order, this expression can be represented in the form

h fl/2

Cx, = —§ (ph(z)aWldz. (2.109)

* J1/2

Consideration of expression (2.109) shows that for a fixed lift coefficient the induced drag coefficient is of the order of О(h0) and, in extreme proximity to the ground, diminishes in direct proportion to the relative ground clearance.

Sometimes it is practical to be able to evaluate the suction force contribution to the induced drag. The magnitude of this force is defined by the perturbation velocities near the leading edge. As demonstrated by Be- lotserkovsky and Scripatch [130], the leading edge flow is close to that in two-dimensions in the plane, normal to the leading edge planform contour.

= ^ [ A2(l, t)cos(v, x)dl = ^ [ A2{l, t)dz. (2.111) ^ Jі ^ Jі Within the theory of the lifting surface in the extreme ground effect, the perturbation velocity in immediate vicinity of the leading edge is given by expression (2.57) и < 0. (2.112) dv у/-2*-hev V ‘ Comparing expressions (2.110) and (2.112) and employing formula (2.111), one can derive the following formula for the suction force coefficient on a wing in the ground effect:

T, . (2.113) -i/2 h*(z, t) The expression for a was obtained by matching and is represented by formula (2.70).

Near the edge, all components of the perturbation velocity can be shown to be finite with the exception of component u„, which is normal to the planform contour and lies in the plane tangent to the lifting surface. If the behavior of uv is described by the relationship

Comment on the Definition of the Leading and Trailing Edges in a Nonlinear Formulation. So far the notions of the leading (side) edge and trailing edges have been dealt with without attention to the questions: Where does the transition lie between these and how can we determine the position of the corresponding transition point? It should be said that such transition points may be fixed a priori by the geometry of the planform, especially if its tips are sharp; see Tuck [53]. Otherwise, when the planform contour is suffi­ciently smooth, the position of the transition point is not known in advance, and its determination becomes part of the flow problem. In the nonlinear case, this transition does not necessarily occur at the wing tips, corresponding to the maximum local span.

Following Newman [54], one can define the transition point as that where both leading edge and trailing edge channel flow boundary conditions are ful­filled simultaneously. To the lowest order of 0(1), it implies that at the point (xt, zt) Є l nl2, where subscript “T” denotes the transition point, both

(2.115) and (2.116) hold simultaneously. Introducing the normal-tangent lo­cal coordinates (v, r) and designating by x the (least) angle between a tan­gent to the wing’s planform contour and x axis, one can rewrite expressions

(2.115) and (2.116) at the transition point, i. e., for (x, z) = as

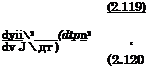<pu =

Substituting (2.118) and (2.119) in (2.120), we finally obtain the following equation for the determining the position of the transition point as part of the lowest order problem solution:

If the perturbations are small (linearized problem), the squares of the pertur­bation: velocity components in (2.120) can be neglected, which results in the following equation:

~q)~ sin Xt = 0. (2.122)

Therefrom

sinxT = 0 at the transition point. (2.123)

It is easy to conclude from (2.123) that for a linearized problem and a smooth wing planform contour, the transition points coincide with the tips of the wing.