Aerodynamic Coefficients for the Fuselage

According to slender body theory, the fuselage does not contribute to lift.

The drag coefficient, CDf0 is calculated with the flat plate formula at Reynolds number Ref = pUlref! r, where lref is the fuselage length. The plate width is estimated to be hf such that the fuselage wetted area is approximately hflref.

The fuselage moment coefficient is now obtained. In slender body theory, the lift of a truncated body of revolution, with base area A = n R2 as reference area, is given by

Cl = 2a (11.12)

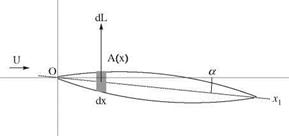
A truncated fuselage that extends from the nose to x will have a lift force given by

12

L =-pU2A(x) 2a (11.13)

A small section of the fuselage from x to x + dx will have a lift force dL (see Fig. 11.3)

dL = pU2a A'(x)dx (11.14)

that will contribute to the pitching moment as

z Fig. 11.3 Moment of a body of revolution at incidence

The minus sign is due to the convention of a positive nose up moment. The integration yields

(11.16)

In the integration by parts, the first term cancels out since the fuselage has zero area at its extremities, and the integral term represents the fuselage volume й f. Hence the fuselage moment reduces to

M, of — pU2 й f a (11.17)

In dimensionless form, using the maximum cross section area A f as reference area, one gets

2й f

Cm, of = — a (11.18)

Aflref

Note that the fuselage moment slope dCMof /da is positive, which is a destabi­lizing moment. In general, the fuselage contribution to the moment is small.

11.2.2 Global Aerodynamic Coefficients for the Glider

The aerodynamic coefficients for the complete configuration cannot be obtained by summing the individual coefficients of each component of the glider, since the reference areas and reference lengths are different. But forces and moments can be summed, and not accounting for the dynamic pressure, one can write

ArefCo — AmCom + At Cot + AfCof (11.20)

Arefl refCM, o — AmcamCM, om + AtcatCM, ot + Aflre fCM ,of (11.21)

The global aerodynamic model for the lift and moment coefficients, is linear. If one chooses as area of reference the sum of the wing and tail areas, the global lift coefficient becomes

AmCL m + AtCLt
Am + At

and the global moment coefficient

It is easy to see that the lift and moment slopes are thus combinations of the wing, tail and fuselage slopes and do not depend on the tail setting angle tt. But the a — 0 coefficients of lift and moment depend on tt.