Conditional analysis techniques: Stochastic estimation

The following exposition is based on that of Adrian (1996). Consider some variable, q, which is unknown, and another vector quantity E = Ei, i = 1..N which is somehow related to q. We are interested in identifying the functional relationship, q = g(E), which provides some approximation of q in terms of E. This kind of estimation of one variable in terms of another is known as stochastic estimation and is widely used in information theory (Papoulis (1984)). When such a relationship cannot be usefully derived from first principals, we frequently revert to statistics: the joint probability density between q and E is:

/qEdфdф = Prob{-0 < q < ф + dф and ф < E < ф + dф}; (167)

the conditional probability density of q given E is

/q|E (Ф|ф)= /Ч/Е(ф)ф) . (168)

Three estimates of q given E are: (1) the maximum likelihood estimate, defined as the most probable value of q given E, i. e. the value at which /qlE is a maximum; (2) the conditional average of q given E, given by the centroid of the conditional probability

< q|E >= J ф/я|Е(ф|фМф;

and, (3) the mean square estimate, i. e. the estimate q = /(E) that min­imises < |q — /(E)| 2 >. It can be shown that the best mean square es­timate of q given E is the conditional average < q|E >. In other words, < |q — /(E)|2 > is a minimum when /(E) =< q|E >.

In this section we outline a technique by which the conditional average can be estimated; in other words we wish to estimate the best estimate: q «< q|E > . The conditional average is approximated by means of a truncated Taylor series expansion about E = 0:

q «<q|E >=/(e) =/(0) + |EЦ + |e2|r + dJL+… (170)

As we do not know the function /(E) we cannot evaluate the derivatives

dn f

dEn and so these are unknowns of the problem. So, considering that the
mean value is zero, (f(0) = 0), the expansion can be written

q «< q|E >= f (E) = AE + BE2 + CE3 + … (171)

and we are required to determine the value of the coefficients A, B, C,… When truncation is performed after the linear term this expression is known as Linear stochastic estimation, when the quadratic term is included we speak of quadratic stochastic estimation, and so on…

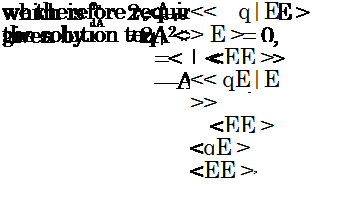
Let us now see how to calculate the coefficients, A, in the case where truncation is performed after the linear term. We have

q « AE,

and we would like to obtain a best minimise the error

where E has been brought inside the conditional average on account of its being constant with respect to the latter, and, in the final step, the conditional average has been performed over all values of E, reducing the conditional average << qE|E >> to the conventional average < qE >.

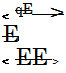So, the linear stochastic estimate of q given some related event E, which provides a best approximation to the conditional average < q|E >, is:

This shows the close relationship between the conditional average and the correlation function < qE >. In the context of aeroacoustics, where E is the
radiated acoustic pressure and q the turbulence velocity, such correlations can be shown to provide an approximation to the integral solution of the acoustic analogy (Lee and Ribner (1972)). An example implementation of this technique is provided in section §4.