CONTRIBUTIONS OF A WING

As previously remarked, on airplanes with tails the wing contributions to the q derivatives are frequently negligible. However, if the wing is highly swept or of low aspect ratio, it may have significant values of CL<i and Cm<i; and of course, on tailless airplanes, the wing supplies the major contribution. The q derivatives of wings alone are therefore of great engineering importance.

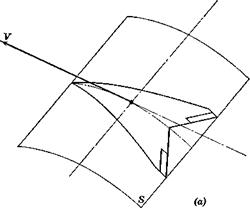
Unfortunately, no simple formulas can be given, because of the complicated dependence on the wing planform and the Mach number. However, the follow­ing discussion of the physical aspects of the flow indicates how linearized wing theory can be applied to the problem. Consider a plane lifting surface, at zero a, with forward speed V and angular velocity q about a spanwise axis (Fig. 7.13). Each point in the wing has a velocity component, relative to the resting atmosphere, of qx normal to the surface. This velocity dis­tribution is shown in the figure for the central and tip chords. Now there is an equivalent cambered wing which would have the identical distribution of velocities normal to its surface when in rectilinear translation at speed F. This is illustrated in Fig. 7.14a. The cross section of the curved surface S is

Fig. 7.13 Wing velocity distribution due to pitching.

(b)

Fig. 7.14 The equivalent cambered wing.

shown in (6). The normal velocity distribution will he the same as in Fig. 7.13

^ T- dz dz q

V — = qx or — = — x дх дх V

and the cross section of S is a parabolic are. In linearized wing theory, both subsonic and supersonic, the boundary condition is the same for the original plane wing with rotation q and the equivalent curved wing in rectilinear flight. The problem of finding the q derivatives then is reduced to that of finding the pressure distribution over the equivalent cambered wing. Because of the form of (7.9,4), the pressures are proportional to qjV. From the pressure distribution, CLa, Gm, and Ghe^ can all be calculated. The derivatives can in principle also be found by experiment, by testing a model of the equivalent wing.

The values obtained by this approach are quasistatic; i. e. they are steady – state values corresponding to a = 0 and a small constant value of q. This implies that the flight path is a circle (as in Fig. 6.32), and hence that the vortex wake is not rectilinear. Now both the linearized theory and the wind – tunnel measurement apply to a straight wake, and to this extent are approximate. Since the values of the derivatives obtained are in the end applied to arbitrary flight paths, as in Fig. 7.116, there is little point in correcting them for the curvature of the wake.

The error involved in the application of the quasistatic derivatives to unsteady flight is not so great as might be expected. It has been shown that, when the flight path is a sine wave, the quasistatic derivatives apply so long as the reduced frequency is small, i. e.

where со is the circular frequency of the pitching oscillation. If l is the wavelength of the flight path, then

so that the condition к < 1 implies that the wavelength must he long compared to the chord, e. g. I > 60c for к < .05.

DEPENDENCE ON h

Because the axis of rotation, Fig. 7.13, passes through the C. G., the results obtained are dependent on h. The nature of this variation is found as

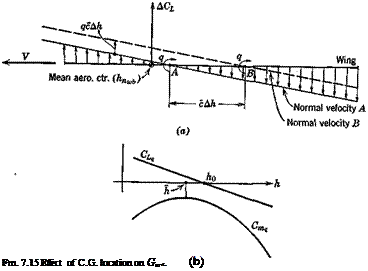
follows. Let the axis of rotation be at A, Fig. 7.15, and let the associated lift and moment be

Ola = OlJ; CmA = CmJ (7.9,5)

Now let the axis of rotation be moved to B, with the change in normal velocity distribution shown on the figure. Since the two normal velocity distributions differ by a constant, (the upward translation qc Ah) the difference between the two pressure distributions is that, associated with a flat plate at angle of attack

oc = -^AA (7.9,6)

V

This angle of attack introduces a lift increment acting at the wing aero­dynamic center of amount

ACl = Gl a = —— AhCL (7.9,7)

" « V x

so that for axis of rotation B,

@lb — ~~ ^La ^4

AGLi_ = -20La Ah

i. e. Gt is linear in h. The incremental moment about В is

■L-‘q

MJm = GLJAh + ACL(hB-hnJ

= [GLqa Ah – 2GLa Ah(hB – hnJ]q

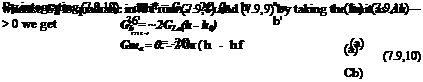
and = [°l, a – 2GBJhB – hnJ] Ah (7.9,9)

The forms of Gl^ and Gm are sketched on Fig. 7.156. h0 is the C. G. position for zero CL, h that for maximum Gm, and Cm is the maximum (least negative) value of Gm<. From (7.9,106) and (7.9,11a), we find

h = i(60 + hnJ (7.9,12)

The linear theory of two-dimensional thin wings gives for supersonic flow:

К = і