Effect of Flight Condition on the Longitudinal Modes of a Subsonic Jet Transport

In Sec. 6.2 we gave the representative characteristic modes of a subsonic jet airplane for a single set of parameters. It is of considerable interest to enquire into how these characteristics are affected by changes in the major flight variables—speed, altitude, angle of climb, and stability margin. It is also of interest to look into the effect of the vertical density gradient in the atmosphere. In this section and by means of exercises we examine some of these effects.

EFFECT OF SPEED AND ALTITUDE

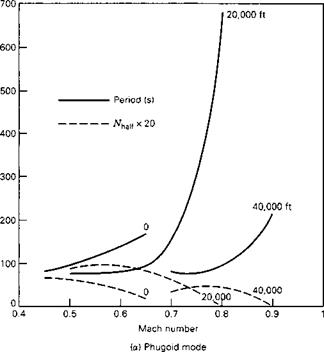
The data in Heffley and Jewel (1972) for the example airplane include several com­parable cases, all having the same geometry, static margin, and gross weight. There are two speeds at sea-level, and three each at 20,000- and 40,000-ft altitudes. The modal periods and damping for these eight cases are displayed in Fig. 6.5. (Since there are so few points, the shapes of the curves are conjectural!) It is an understate­ment to say that there is no simple pattern to these data. It can be said, however, that the phugoid period increases with speed, as predicted by the Lanchester theory, and decreases with altitude at fixed Mach number. The short-period does the opposite, de­creasing with speed and increasing with altitude.

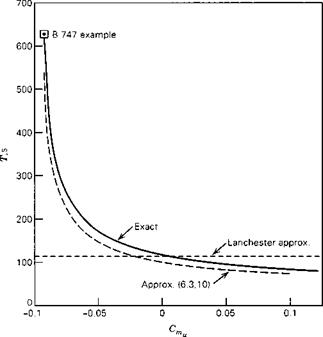
The most striking feature of the data is the sudden and large increase in the phugoid period at high Mach number at the two higher altitudes. This phenomenon is a result of a loss of true static stability at these Mach numbers brought about by a negative value of Cmu, which has the effect of reducing E in (6.4,2). This happens be­cause this large aircraft is necessarily quite flexible, and because at these Mach num­bers it is entering the transonic regime, where air compressibility leads to substantial alterations in the aerodynamic pressure distribution. To show that Cmu is the reason for the behavior of the graphs, we vary it over a large range for the flight condition M = 0.8 and 20,000-ft altitude. Figure 6.6 shows the result and substantiates the impor­tant role of this derivative. In fact, from (6.4,4) we calculate that E = 0 when Cmu = -0.0968, a value only 4% more negative than that of the example at the given flight

(6) Short-period mode

Figure 6.5 Variation of longitudinal modes with speed and altitude. (a) Phugoid mode. (b) Short – period mode.

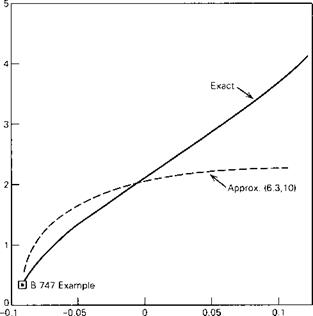
condition. Thus at this point the airplane would be very close to the static stability boundary, at which the period would go asymptotically to