Equations of Motion for Hypersonic Attached Viscous Flow

We study now the equations of motion for hypersonic attached viscous flow. We find these equations in the same way in which we found the boundary- layer equations in Sub-Section 7.1.3, but now making the pressure dimen­sionless with pref instead of pref v2ef. We assume perfect gas and keep the bulk viscosity к because the terms containing it will not drop out, unless we go to the boundary-layer limit. For convenience we consider only the two­dimensional case and keep again x as coordinate tangential to the surface and y normal to it. The equations are written dimensionless, but we leave

the prime away. Higher order terms regarding the reference Reynolds number are neglected. The extension to three dimensions is straight forward.

In analogy to eqs. (7.5), (7.16), (7.17), and (7.20) we find first the (un­changed) continuity equation

dpu dpv

dx R dy

then the Navier-Stokes equations

and finally the energy equation, where on purpose the Eckert number is not employed

It is obvious that these equations reduce to the boundary-layer equations, see (7.36) to (7.40), albeit with some different co-factors, if the Reynolds number Reref is very large and the ratio ‘M^ef ’ to ‘Reref’ very small:

M? ef

-^«F

Reref

This means that if eq. (7.78) is true, the flow is of boundary-layer type, because the pressure is constant in the direction normal to the surface.

If on the other hand

we must expect a pressure not constant in direction normal to the surface. If this happens on a flat vehicle configuration element, in the limiting case on a flat plate, we speak of hypersonic viscous interaction, which we treat in Section 9.3, where we will meet again the term МД, f /Reref, respectively its square root Mref j y/Reref.

We study now in more detail the characteristic properties of eqs. (7.74) to (7.77) in order to get clues regarding the kind of possible numerical com­putation schemes for such flows.

We introduce again characteristic manifolds p [13] for derivatives like in eq. (7.41). To make the problem treatable, we simplify the governing equa­tions by keeping only the leading terms in the equations, omitting the co­factors containing Mref, Reref, 7, and Prref, and by assuming constant transport properties p, к and heat capacity cp:

du dp dv dp

Ртг + !1V + Pw~ + v— = 0,

dx dx dy dy

du du dp dp d2u

Pu~:—— к pvw~ = ~w~t.—– к

dx dy dp dx dy2

dv dv dp dp d2v

PlW к Pvw~ = — к A‘Tyvy,

dx dy dp dy dy2

( dT dT d2T

cp pu— + pv— = k— + CWT + DWT,

dx dy dy2

with CWT and DWT being abbreviations of the compression and dissipation work terms, respectively.

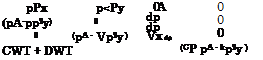The characteristic matrix then reads, with px and py the characteristic directions of the problem [13]

upx + vpy. From this we obtain:

and finally with A = upx + vpy = 0, eq. (7.46), and by identifying dp/dp = a2 with the speed of sound

C = p p к ip у [(г/2 – gr_)ip2c + 2 uvipxspy + (v2 – a2)y>2] = 0. (7.86)

The term in this equation coming from the pressure gradient term in eq. (7.75) is underlined. Because we have assumed constant viscosity, no coupling of the continuity equation and the momentum equations with the energy equation exists. Hence from the latter only the convective term and the thermal conduction term in у-direction are reflected in eqs. (7.85) and (7.86), respectively.

We find thus a four-fold characteristic in y-direction and in the angular brackets elliptic characteristics for subsonic flow and hyperbolic ones for su­personic flow. If the underlined pressure-gradient/speed-of-sound term would be omitted, we would get in the angular brackets for all flow velocities hyper­bolic characteristics [18]. The system of equations (7.74) to (7.77) without the terms, which are of smaller order of magnitude, and without the pressure – gradient term in eq. (7.75), thus would constitute a linearized system of equations for the description of a weakly disturbed hypersonic flow with u2 ^ a2, v = O(a). If the pressure-gradient term in eq. (7.76) would be zero, the whole equation would disappear, and we would get the boundary-layer equations for hypersonic flows.

If we accept the simplifications made in the equations of motion and those made additionally in order to investigate the characteristic properties of the system of equations, we get the result that the equations of motion without the second-order terms in ж-direction are essentially of elliptic nature for subsonic flows and of hyperbolic nature for supersonic flows.

If the problem at hand permits it, the pressure-gradient term in eq. (7.75) can be omitted. This is possible for flows where

(7’87)

In this case the system of equations is of hyperpolic/parabolic type in the whole flow domain and can be solved as initial/boundary value problem with a space-marching numerical scheme, Section 9.3. If the term cannot be omitted, a parabolization scheme, for instance that of Vigneron et al. [19], must be employed, otherwise the solution process will become unstable.11 [93] [94]