Indicial Response: Wagner’s Problem

Theodorsen’s lift deficiency approach has found use in many problems in both fixed-wing and helicopter aeroelasticity. However, for a rotor analysis Theodorsen’s theory is somewhat less useful because the nonsteady value of velocity at the blade elements, V = Uj(y, jf), means that the argument к (the reduced frequency) is, strictly speaking, an ambiguous parameter. Therefore, a theory formulated in the time domain is more general and is usually more useful. Wagner (1925) has obtained a solution for the so-called indicial lift on a thin-airfoil undergoing a transient step change in AoA in an incompressible flow.[30] The transient chordwise pressure loading is given by

ACp(x, s) 4 /——— з 11 — x

————– = — 5(f)>/(l – x)x + 40(j)J ——, (8.46)

a V у x

where <fi(s) is called Wagner’s function and, by analogy with the Theodorsen function, accounts for the effects of the shed wake. As defined previously in Eq. 8.4, the variable s represents the distance traveled by the airfoil in semi-chords. The first term in Eq. 8.46 is the apparent mass contribution, which for a step input appears as a Dirac-delta function S(t). The corresponding result for an indicial change in pitch rate about the leading edge is given by

ACp(x, j) = ^(1+2jc)V(l -*)*+( 30(5) – l) УЦ^-НЦ/(1 – ф. (8.47)

Again, the first term is an apparent mass term, with the second term being circulatory in nature and is affected by the shed wake. The third term is a quasi-steady term, with an analogous term also appearing in Theodorsen’s result.

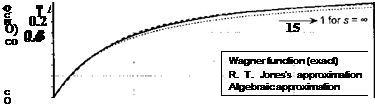
Wagner’s function, 0(s), is known exactly [see, for example, Lomax (1968)] and is plotted in Fig. 8.19. Notice that the noncirculatory or apparent mass loading is responsible for the initial infinite pulse at 5 = 0. Thereafter, the function builds asymptotically from one half to a final value of unity as s —> oo. In Wagner’s problem, the aerodynamic center is at mid-chord at s = 0 and moves immediately to the 1 /4-chord for s > 0. The resulting variation in the lift coefficient for a step change in angle of attack, a, can be written as

CKO = ^S(t) + 271 a<Ks), (8.48)

where 2na is the steady-state lift coefficient, as given by steady thin-airfoil theory.

For rotor analyses, the indicial lift response makes a useful starting point in the devel­opment of a general time domain unsteady aerodynamic theory. If the indicial response is known, then the unsteady loads to arbitrary changes in AoA can be obtained through the superposition of indicial aerodynamic responses using the Duhamel integral. Consider a general system in response to a general forcing function f(t), t > 0. If the indicial response

Distance traveled in semi-chords, s

Figure 8.19 Wagner’s function for a step change in angle of attack.

ф of the system is known, then the output y(t) of the system can be written in terms of Duhamel’s integral as

(8.49)

See Section 8.14 and Bisplinghoff et al. (1955) or von Karman & Biot (1940) for details. In Eq. 8.49, cr is simply a dummy time variable of integration, and the first term is related to the initial condition from which subsequent inputs are applied. By analogy with Eq. 8.49, the circulatory part of the lift coefficient, Cf, in response to an arbitrary variation in AoA can now be written in terms of the Wagner function as

where ae simply represents an effective AoA and contains within it all of the time history effects on the lift because of the influence of the shed wake. Notice that if V = constant, then s = 2 Vt/с. In addition, the appropriate apparent mass terms must be added to get the total lift. For incompressible flow, however, the apparent mass terms are proportional to the instantaneous motion, so they all conveniently appear outside the Duhamel integral.

The Duhamel integral in Eq. 8.50 can be solved analytically or numerically. Analytical solutions are mostly restricted to simple forcing functions, and numerical methods must be employed in the general case. The main difficulty in solving Duhamel’s integral is, however, with the Wagner function itself. Although the Wagner function is known exactly, its evaluation is not in a convenient analytic form. Therefore, it is usually replaced by a simple exponential or algebraic approximation. When this is done, a whole series of practical numerical tools for computing the unsteady aerodynamics can be unleashed. One approximation to the Wagner function, attributed to R. T. Jones (1938, 1940), is written as a two term exponential series with four coefficients, that is,

as shown in Fig. 8.19. This approximation is found to agree with the exact solution to an accuracy that is within 1%. Another approximation to the Wagner function is attributed to W. P. Jones (1945); here

0(j) ^ 1.0 – 0.165е_0 04ь – 0.335e_0-32*

In each case it will be noted that A + A 2 — 0.5, according to Wagner’s exact result.

The main advantage of using the exponential approximation is that it has a simple Laplace transform. While the exponential behavior of the Wagner function is not an ex­act representation of the physical behavior, it is usually sufficiently accurate for practical calculations.[31] An alternative algebraic approximation to the Wagner function suggested by Garrick (1938) is

(8.53)

which, although not as accurate as the exponential approximation except in the limit as s -> oo, it agrees with both the exact solution and with the exponential approximation to within 2% accuracy.