Measurement of flow speed by pressures

The speed, U, in a gas can be calculated from the ratio between stagnation pressure, p0, and static pressure, p, using the relationship valid for a thermally and calorically perfect gas:

where M is the Mach number, у is the ratio of specific heats at constant pressure and constant volume, T the static temperature and R the gas constant, ratio between the universal gas constant and the molecular weight of the gas.

From Equation (2.1), the speed U is obtained:

The calculation of speed hence requires the measure of two pressures, p0 and p, and the measure of the static temperature of the stream, which is impossible to obtain, as we shall see, when the Mach number is high; it is easier in this case to calculate the Mach number, which is a function of pressures only:

In the case of flow at low Mach numbers (M << 1), Equation (2.1) can be expressed in a power series of M2 (U2) as follows:

This yields, by truncating the series at the second term:

p0 = p +

which is the Bernoulli equation for an incompressible flow. This equation underestimates the stagnation pressure compared to Equation (2.1) (the next terms in the series, all positive, are ignored) and hence for the same p0 and p, provides a higher speed.

In this scheme, the speed can be calculated, once the density (constant) is known, from the difference between the stagnation pressure and the static pressure (dynamic pressure, q) according to the equation:

From Figure 2.1, which shows the ratio, Equation (2.4), between the speed calculated with Equation (2.3) and the speed calculated with Equation (2.2), we see that Equation (2.3), strictly valid only for M = 0, can be used, accepting an error of less than 1% up to M = 0.3, or up to M = 0.4, if an error of 2% can be accepted.

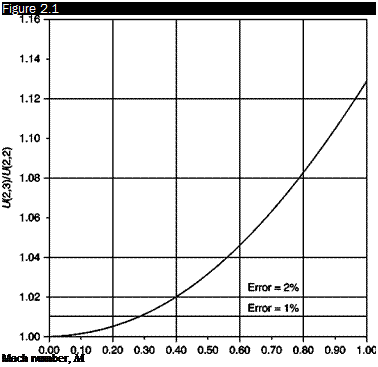Ratio of speed calculated by the Bernoulli theorem and true speed for у = 1.4

In compressible flows, as can easily be seen from Equation (2.1), the dynamic pressure is no longer equal to q = pV2/2 but the latter term is still used to define pressure coefficient and aerodynamic forces coefficients.

Speed of a stream can then be measured on whatever body is immersed in the stream because on it both the stagnation pressure, in the stagnation point, and the pressure of the undisturbed stream can be found. For example, on an infinite cylinder of circular cross-section immersed in a non-viscous and incompressible flow with velocity Vx perpendicular to axis of the cylinder (Figure 2.2): defining as pressure coefficient the ratio

C = p-p, p pU1 ± 2

■ Cp = 1 (p = p0 at the stagnation points) at a = 0° and 180°

■ Cp = 0 (p = px) at a = ±30° and ±150°

On a sphere:

■ Cp = 1 (p = p0 at the stagnation points) at a = 0° and 180°

■ Cp = 0 (p = px) at a = ±40° and a = ±140°

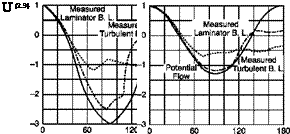Diagrams of pressure coefficient, Cp, on a cylinder and a sphere in a theoretical potential flow, and in real laminar and turbulent regimes

Sphere

In practice, a flow is never potential: if the Reynolds number is large but not infinite, a boundary layer will exist all around the body; nevertheless, the pressure on the body will be the same as that outside the

boundary layer because of the relationship — = 0. Therefore the

dy

distribution of pressure in the field outside the boundary layer can be detected through orifices made on the surface of the body. It must be noted, however, that the distribution of pressure on the body is different from that of potential flow; in fact, in the wake, the recovered pressure is lower than the stagnation pressure. Furthermore, the position of the points where the pressure is equal to pm is moved downstream about 5°; pressure on the afterbody is strongly influenced by the nature of the boundary layer and hence by the location of the boundary layer separation.

However, there are special cases, such as measuring the speed profile within the boundary layer itself with very small probes and in the presence of very low speed: in these cases the Reynolds number referred to the size of the probe is very small and the flow in the proximity of the probe must be considered viscous and corrections to measured pressures will be made (cf. Section 2.3.5).

It can be noted that measuring p0 and pm on blunt bodies, such as circular cylinders and spheres, is impractical both because of the large dimensions, leading to a poor resolution, and because of the great variability of the pressure on the body with flow direction. Tubular probes of smaller size and lower sensitivity to direction are therefore preferred.

In some cases, the measurement of speed can be simplified:

■ In a wind tunnel, the stagnation pressure of the undisturbed stream can be known by measuring the static pressure in the settling chamber of the wind tunnel, where the speed is low enough. Similarly, the static pressure of the undisturbed stream can be measured in an orifice drilled in the wall in the entrance station of the test chamber. From the two measures the Mach number of the tunnel can be determined by Equations (2.2) or (2.3), without introducing probes into the stream.

The measure will, however, be slightly wrong because the stagnation pressure is not exactly the same in the settling chamber and in the test chamber.

■ In a subsonic free jet, static pressure must be equal to ambient pressure and can be measured with a barometer; to measure the speed profile in the jet, it is then sufficient to measure the profile of the stagnation pressure.

■ Similarly, as the static pressure in each section of a straight tube is constant and can be measured in an orifice drilled in the wall, the speed profile in a section can be obtained by taking only the measure­ments of the stagnation pressure.