Pressure, density and temperature ratios along a streamline in isentropic flow

Occasionally, a further manipulation of Eqn (6.17) is of more use. Rearrangement gives successively

since it follows from the relationship (6.1) for isentropic processes that P1/P2 = W/92)7.

Finally, with al = (1Р2ІР2) this equation can be rearranged to give,

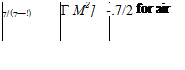If conditions 1 refer to stagnation or reservoir conditions, щ = 0, p — po, the pressure ratio is

Po P*

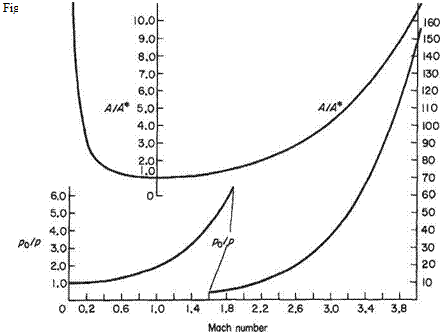
where the quantity without suffix refers to any point in the flow. This ratio is plotted on Fig. 6.2 over the Mach number range 0-4. More particularly, taking the ratio between the pressure in the reservoir and the throat, where M = M* = 1,

Note that this is the minimum pressure ratio that will permit sonic flow. A greater value is required to produce supersonic flow. The ratios of the other parameters follow from Eqns (6.18) and (6.2):

P2 P2j L 2	(6.19)
P L 2 J	(6.19a)
до Г7+ll1/(7-1) ’* = 7 г =1.58 for airflow P* L 2 J	(6.19b)

T (p\b 1)/7 7 – 1 «2 – »1 T2 pi) 2 a	(6.20)
^=i+7:V T 2	(6.20a)
^ * = 1.2 for airflow T* 2	(6.20b)

Example 6.1 In streamline airflow near the upper surface of an aeroplane wing the velocity just outside the boundary layer changes from 257 km h-1 at a point A near the leading edge to 466kmh_1 at a point В to the rear of A. If the temperature at A is 281К calculate the temperature at B. Take 7 = 1.4. Find also the value of the local Mach number at the point B.

(LU)

Assume that the flow outside the boundary layer approximates closely to quasi-one-dimen­sional, isentropic flow.

Then

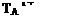Tb, , 7~ 1 ma ~ UB

«a

5 aA

aK = 12Ay/l and ГА = 8 + 273 = 281К

да = 1215kmh_1

ы «А 257

"Л-^=Ш5“0212

— = = 0.385

aA 1215

^ = 1 + ~[0.2122 – 0.3852] = 0.979 = 1 – 0.021 ГА 5

Therefore

7b = 0.979 x 281 = 275 К = temperature at В яв = 72.4/275 = 1200 km IT1

466: = 0.386

Example 6.2 An aerofoil is tested in a high-speed wind tunnel at a Mach number of 0.7 and at a point on the upper surface the pressure drop is found to be numerically equal to twice the stagnation pressure of the undisturbed stream. Calculate from first principles the Mach number found just outside the boundary layer at the point concerned. Take 7 = 1.4. (LU)

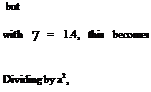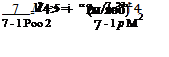Let suffix cxi refer to the undisturbed stream. Then, from above,

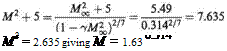and Eqn (i) gives