Principles of Quasi-Steady Thin-Airfoil Theory
The unsteady airfoil problem can be tackled initially starting from the classical, incompressible, steady, thin-airfoil theory, which is described in Section 14.8. This is equivalent to setting all the unsteady terms in the governing flow equations equal to zero and will be called the quasi-steady problem. At the most elementary level it is convenient to think of oscillatory motion of the airfoil. This motion can be decomposed into contributions associated with AoA (which is equivalent to a pure plunging motion) and contributions associated with pitching (which includes contributions from both AoA and pitch rate) – see Fig. 8.4.
|
|
|
Figure 8.4 Unsteady oscillatory forcing can be considered to have contributions from both plunging and pitching motion, including rate terms. |
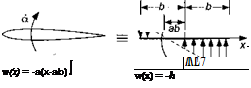 |
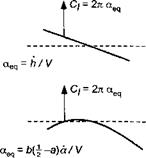 |
Figure 8.5 Velocity perturbation normal to chord and effective induced camber for plunge velocity and pitch rate about an axis located at 1 /4-chord.
The unsteady motion of the airfoil produces a distribution of perturbation velocity normal to the chord, for which a solution to the vortex sheet strength on the airfoil, уь, can be found to maintain flow tangency on the chordline. An angle of attack, a, or plunge velocity, h, produces a uniform velocity perturbation w that is normal to the chord, as shown in Fig. 8.5. For an AoA perturbation, w{x) = Va = constant. Similarly, for a steady plunge velocity, w(x) = —h = constant. The pitch-rate term produces a linear variation in normal perturbation velocity. For a pitch rate imposed about an axis at a semi-chords from the mid-chord, then w(x) = —a(x — ab), so that the induced camber is a parabolic arc, as also
о c
M1UW11 111 I’lg. O. J.
The quasi-steady contribution to the airloads follows directly from thin-airfoil theory (Section 14.8) using the following solutions for the Fourier harmonics:
Ao = ot — — J and An = —J cos nOdO, (8.5)
where x = —b cos 9 based on a coordinate system at mid-chord. The results for this problem are summarized in Table 8.1. The quasi-steady lift and pitching moment are then
![]() я ab
я ab
47’
and
![]() (8.8)
(8.8)
For a pitching axis at the 1 /4-chord (a = — 1 /2), the term inside the square brackets in Eq. 8.6 will be seen to be the effective AoA at the 3/4-chord. If a = 1/2 then no lift is produced by pitch rate about 3/4-chord, and for this reason the 3/4-chord point is sometimes called the rear neutral point. Also, note that the pitching moment about the 1 /4-chord resulting from the pitch rate contribution is independent of the pitch axis location, a (see Question 8.2).