Sharp-Edged Gust: Kiissner’s Problem

In a rotor flow field, the rotor wake (and specifically the tip vortices) produces a highly nonuniform induced velocity field across the plane of the rotor disk. Therefore, a typical blade element encounters a nonuniform vertical upwash/downwash as it rotates in this field. It is, therefore, important to distinguish properly the effects on the airloads arising from AoA changes from blade motion (in effect, a plunging and pitching motion at the blade element) from the effects resulting from the rotor wake-induced velocity field (in effect, a vertical gust velocity normal to the blade element). This distinction has important effects on the resulting airloads and should not be overlooked in the mathematical modeling of helicopter rotor problems.

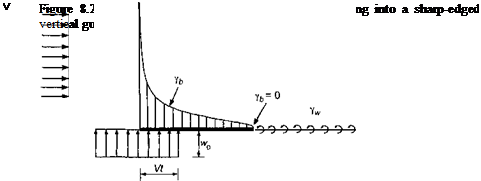
The problem of finding the transient lift response on a thin-airfoil entering a sharp-edged vertical gust (that is, a vertical upwash velocity) was first tackled by Kiissner (1935) and properly solved by von Karman and Sears (1938). In this problem, the upwash velocity, wg, is defined relative to an axis at the leading edge as

(8.54)

as shown in Fig. 8.20. Recall that, in Wagner’s problem, the AoA changes instantaneously over the whole chord at s — 0. In Kussner’s problem, however, the quasi-steady AoA changes progressively as the airfoil penetrates into the gust front. At s = 2, the airfoil becomes fully immersed in the gust. The resulting variation in the lift coefficient can be written in a similar way to Wagner’s solution such that

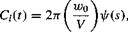(8.55)

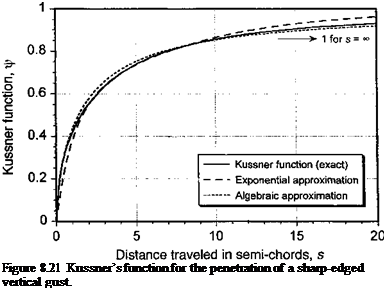
where yjs(s) is known as Kiissner’s function and is plotted in Fig. 8.21. Compared to the Wagner function, which has an initial value of one-half, it will be seen that the Kiissner function builds from an initial value of zero and asymptotes to unity for s -» oo. Kussner’s function is also known exactly, albeit not in a convenient analytic form. Von Karman & Sears (1938) also showed that the aerodynamic center always acts at the 1/4-chord of the airfoil for all s. This is perhaps a surprising result, but it has been verified experimentally – see Sears & Sparks (1941).

The Kiissner function can be used with the Duhamel superposition integral to find the lift response to an arbitrary vertical upwash field, where the lift coefficient can now be obtained using

2тг ( Ґ dwJa)

Q(t) = — ( wg(0)l/(s) + j^ ~ v)dcr

Notice that this equation is analogous to the result for the lift resulting from arbitrary varia­tions in angle of attack, as given previously in Eq. 8.50, but with a different indicial function being used. To enable practical calculations using Duhamei superposition, the Kiissner func­tion, like the Wagner function, is usually replaced by an exponential approximation. One approximation is given by Sears & Sparks (1941) as

f(s) « 1 – 0.5e~ai3s – 0.5e~1(k, (8.57)

which is shown in Fig. 8.21. Alternatively, an algebraic approximation that is sometimes used for the Kiissner function is

which is given by Bisplinghoff et al. (1955). Neither approximation represents the correct vertical tangent of the Js curve at s = 0, but this is of no practical significance.