State-Space Solution for Arbitrary Motion

For some applications, it is more convenient if the unsteady aerodynamic model is written in the form of differential equations (i. e., in state-space or state-variable form). The differential equations describing the unsteady aerodynamics can then be directly appended to the structural dynamic equations governing the airfoil or blade motion. One advantage of this approach is that the stability of an aeroelastic problem for a wing section or rotor blade can then be obtained by formulating it as an eigenvalue problem or using a Floquet stability analysis [see Johnson (1980)]. Alternatively, the problems can be studied by time integration of the governing equations using standard numerical algorithms.

One of the most fundamental concepts associated with the description of any dynamic system, aerodynamic or otherwise, is the state of the system. The state describes the internal behavior of that system and is simply the information required at a given instant in time to allow the determination of the outputs from the system given future inputs. In other words, the state of the system determines its present condition; it is represented by a set of appropriately chosen variables describing the internal mechanics of the system. These variables are called the state variables and define an n -dimensional vector space x called the state-space in which one coordinate is defined by each of the state variables x, x2, xn. A general nth order differential system with m inputs and p outputs may be represented by n first-order differential equations

x = Ax + Bu (8.100)

with the output equations

у = Cx + Du, (8.101)

where x = dx/dt u = и;,’ і = 1, 2, …, m are the system inputs, and the у = yt, і = 1, 2,…, p are the system outputs, x = Хі, і = 1, 2,…, n are the states of the system. See Franklin et al. (1994) for more information about this approach.

The state equations describing the behavior of a 2-D unsteady airfoil can be obtained through direct application of Laplace transform methods to the indicial response. Consider the indicial lift response, ф, which is to be approximated by the exponential function given previously by Eq. 8.76. This function can be written in the time domain as

0(0 = 1.0 – Axe~b^> – A2e~b2(^>. (8.102)

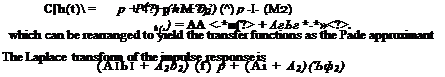Initially, let 0(0) = 0 = 1 — Ai — A2. Then the corresponding impulse response, h(t), is given by

From this transfer function, the lift response to an input a(t) can be directly written in state-space form as

(8.106)

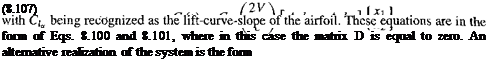and the output equation for the lift coefficient is

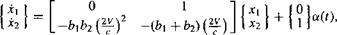(8.108)

and the corresponding equation for the lift coefficient is

cm = cla[bxb2 (^)2 (Ab + A2b2) (f )]{XX }.

For a nonzero initial condition, such as when using the Wagner function approximation, the form of these equations is only slightly different. In this case

(8.110)

id the equation for the lift coefficient is

Ci(t) — Cta |A] + A2)bb2 (^) (Ab + A2b2) (^) ] I I

+ C/o(l — A — A2) ot(t).

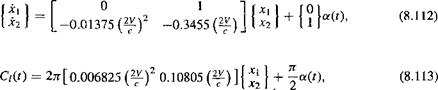For example, if R. T. Jones’s approximation to the Wagner function is used (Eq. 8.51), then after substituting the numerical values of the coefficients we get

where Cia = 2tt. The extra term 7ra/2 on the right-hand side of the above equation arises be-

1 /2. Conversely, if we apply a unit step input to the above state-space equations and set the initial states to be zero [i. e., a(t) = 1 for t > 0 and xi(0) = *2(0) = 0], the resulting response is exactly Jones’s approximation to the Wagner function (see Question 8.11). In fact, it is clear that the Theodorsen solution, the Wagner solution with Duhamel super­position, and the above state-space model are simply different mathematical realizations of the same aerodynamic system. Friedmann (1985), Dinyavari & Friedmann (1986), and Leishman & Nguyen (1990) describe state-space unsteady aerodynamic models of 2-D airfoil sections using Jones’s approximation to the Wagner function for the incompressible flow case. Friedmann (1985) describes a more general, but still approximate, state-space

realization of Loewy’s function (Section 8.8). This is done by representing Loewy’s exact lift transfer function as a higher-order Pade approximation – see also Vepa (1976).