Static Stability

One of the most common design mistake made by student teams is a misplacement of the center of gravity. This results in the pilot having to constantly act on the tail deflection to maintain the airplane aloft or, in the worst case, ground rolling is immediately followed by a nose up and stall at take-off with likely loss of the airplane. The study of static stability clearly demonstrates a sufficient requirement for stability. For simplicity, we use a linear model obtained from the above model by assuming the following linear behavior of the coefficients

Cl (a) = a + Clo(tt), Cm, o (a) = a + Cm, o0 (tt) (11.46)

d a d a

Here the lift and moment slopes are assumed constant as well as the a = 0 lift and moment coefficients which depend only on the tail flap setting angle tt. We further assume small angles a and в and neglect the thrust in the first equation, Eq. (11.45). The system reduces to

Cl – Cw = 0

Cd – Ct + в Cw = 0 (11.47)

Cm, o + xfCw = 0

1ref

Substitution of Cw from the first equation into the third one yields an equation

for aeq

X

CM, o (aeq) + – CL (aeq) = CM, cg (aeq) = 0 (11.48)

Iref

representing the moment about the center of gravity. This is easily solved with the linear model as

Cm, o0(tt) + XcgfCL0(tt)

aeq to) =————- (1L49)

da + Iref da

The equilibrium incidence is controlled by the tail setting angle.

The equilibrium velocity is obtained from the definition of Cw and the first equa­tion, now that the lift Cl, eq = Cl (aeq) is known

Veq(tt) = J— Є

2 P Aref eL, eq

Finally, knowing the velocity and incidence, the coefficients of drag CD, eq and thrust CT, eq can be calculated and the slope of the trajectory evaluated as

в„ (tt) = CT’eq~ CD‘q (11.51)

eL, eq

Note that if Ct, eq < Cd eq the slope is negative and the trajectory is down. This is the case for a glider or when the engine is turned off since Ct = 0. This simple system also shows that for a glider, if one neglects the change in Reynolds number hence in CD0(Re), adding or subtracting mass at the center of gravity does not affect the equilibrium incidence aeq nor the slope angle вщ, and only affects the velocity on the trajectory which will change proportionally to VW".

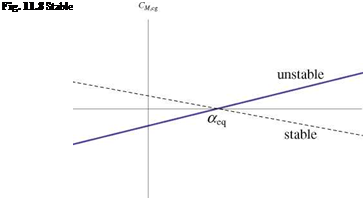
Considering the moment of the aerodynamic forces at the center of gravity elim­inates the action of the weight. It is easy to show that, for static stability, one needs to satisfy the inequality

dCM^ (a) < 0 (11.52)

da

Indeed, if a perturbation, say a gust of wind, deviates the incidence from the equilibrium incidence by a Aa > 0 or nose up, a negative pitching or nose down moment ACM, cg < 0 is needed to restore the equilibrium incidence, and vice-versa, Fig. 11.8.

Another important point for the aerodynamic static stability of an airplane is the aerodynamic center (or neutral point) of the configuration. It is located between the aerodynamic center of the main wing and the aerodynamic center of the tail, proportionally to their areas and lift slopes as given by the linear model (neglecting the small fuselage contribution)

Note that its location is independent of tt. It is defined as the point about which the moment of the aerodynamic forces is independent of incidence, i. e. it satisfies

dC^O + Xa^dCb = 0 (11.54)

da lref da

Taking the derivative of the moment equation about the center of gravity, CM, cg (a) and satisfying the static stability inequality reads

Fig. 11.9 UC Davis entry at the 2006 aero design west competition

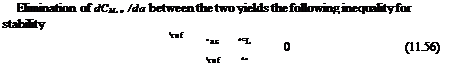Since the lift slope is positive, the condition reduces to

In other words, the center of gravity must be in front of the aerodynamic cen­ter. This is one of the most important design requirements, that was fulfilled as always in the model airplane of 2006, Fig. 11.9. The static margin defines the distance xa. c. – xc. g. as a percentage of the reference length as