. Theodorsen’s Theory

Theodeorsen’s theory, which is widely used by fixed-wing analysts, forms one root for many of the unsteady aerodynamic solution methods used for helicopter analysis. The problem of finding the airloads on an oscillating airfoil was first tackled by Glauert (1929), but was properly solved by Theodorsen (1935). Theodorsen’s approach gives a solution to the unsteady airloads on a 2-D harmonically oscillated airfoil in inviscid, incompressible flow, and subject to small disturbance assumptions. The basic model is shown in Fig. 8.6. Both the airfoil and its shed wake are represented by a vortex sheet, with the shed wake extending as a planar surface from the trailing edge downstream to infinity. The shed wake comprises countercirculation that is shed at the airfoil trailing edge and is convected downstream at the free stream velocity. The assumption of a planar wake is justified if the AoA disturbances remain relatively small. As with the standard quasi-steady thin-airfoil theory, the bound vorticity, уь, can sustain a pressure difference and, therefore, a lift force. The wake vorticity, yw, however, must be force free with zero net pressure jump over the sheet.

Theodoisen’s problem was tu obtain the solution for the loading, y^, on the airfoil surface under harmonic forcing conditions. The governing integral equation is

± Г dx+— Г ^iHdx

2n Jo (x – X0) 27Г Jc (x – x0)

where w is the downwash on the airfoil surface. This equation must be solved subject to invoking the Kutta condition at the trailing edge [i. e., уь(с, t) = 0]. There is also a connection to be drawn between the change in circulation about the airfoil and the circulation shed into

the wake. Conservation of circulation requires that

Assuming that the shed vortices are convected at the free stream velocity, V, this gives dx = Vdt and so

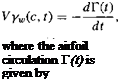
(8.11)

(8.12)

This wake vorticity changes the downwash velocity over the airfoil and, therefore, the loads on the airfoil are also affected. So long as the circulation about the airfoil is changing with respect to time, circulation is continuously shed into the wake and will continuously affect the aerodynamic loads on the airfoil. In the limit as the forcing becomes zero, the shed wake vorticity cast off the trailing edge of the airfoil becomes zero, and the remaining circulation in the wake convects downstream to infinity. In this case, the problem is modeled by the standard quasi-steady thin-airfoil theory.

The unsteady problem posed above is certainly not trivial to solve, but for simple har­monic motion the solution is given by Theodorsen (1935) in a form that represents a transfer function between the forcing (angle of attack) and the aerodynamic response (pressure dis­tribution, lift, and pitching moment). Theodorsen’s approach is summarized by Bisplinghoff et al. (1955) and by another approach attributed to Schwarz. See also Bramwell (1976) and Johnson (1980) for a good exposition of the theory. For a general motion, where an airfoil of chord c = 2b is undergoing a combination of pitching (a, dr) and plunging (h) motion in a flow of steady velocity V, Theodorsen gives for the lift

(8.13)

where a is the pitch axis location relative to the mid-chord of the airfoil and is measured in terms of semi-chords. The corresponding moment about mid-chord is

(8.14)

The first set of terms in Eqs. 8.13 and 8.14 result from flow acceleration effects (i. e., a noncirculatory or apparent mass effect). The second terms arise from the creation of circulation about the airfoil (i. e., a circulatory effect). The circulatory term C(k) = F(k) + і G(k) is a complex valued transfer function known as Theodorsen’s function, which accounts for the effects of the shed wake on the unsteady airloads.

The noncirculatory or apparent mass terms arise from the дф/St term contained in the unsteady Bernoulli equation (Kelvin’s equation) [see Karamcheti (1966)] and account

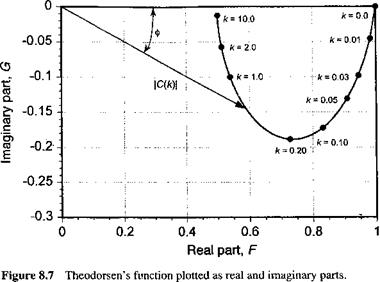It will be appreciated from Fig. 8.7 that Theodorsen’s function serves to introduce an amplitude reduction and phase lag effect on the circulatory part of the lift response compared to the result obtained under quasi-steady conditions. The basic effect can be seen if a pure oscillatory variation in AoA is considered, that is, a = aelwt. In this case2 the circulatory part of the airfoil lift coefficient is given by

Сі = 2л a C(k) = 2л a [F(fc) + iG(k)]. (8.23)

Representative results from the Theodorsen model are shown in Fig. 8.8. For к = 0 the steady-state lift behavior is obtained, that is Q is linearly proportional to a. However, as к is increased, the lift plots develop into hysteresis loops, and these loops rotate such that the amplitude of the lift response (half of the peak-to-peak value) decreases with increasing reduced frequency. These loops are circumvented in a counterclockwise direction such that the lift is lower than the steady value when a is increasing with time and higher than the steady value when a is decreasing with time (i. e., there is a phase lag). Notice that for infinite reduced frequency the circulatory part of the lift amplitude is half that at к = 0 and there is no phase lag angle.