Time-Varying Incident Velocity
The previously described unsteady airfoil solutions have considered the local free stream velocity to be constant. However, in forward flight a typical blade element on a rotor
|
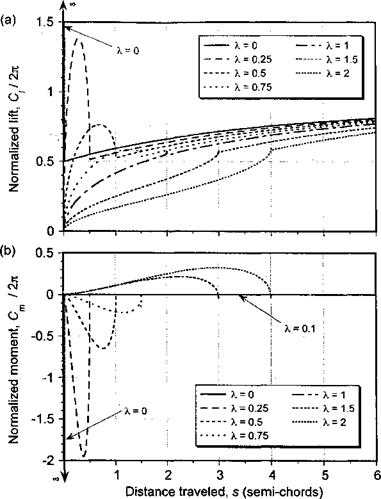
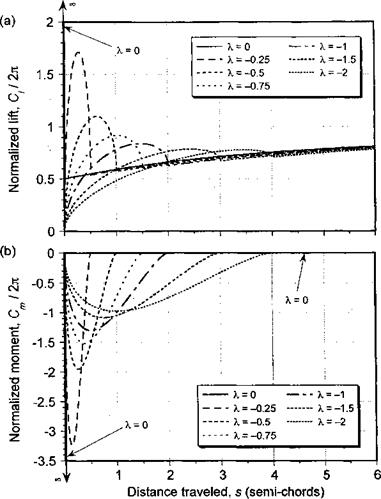
Figure 8.23 Airloads produced for a series of downstream moving sharp-edged vertical gusts, (a) Lift, (b) Pitching moment about 1 /4-chord. |
will encounter a time-varying incident velocity because У = UT(y, VO = Qy+f^QR sin f. Under these conditions, there are additional unsteady aerodynamic effects to be considered. These effects include both noncirculatory and circulatory contributions. With a time-varying incident flow velocity, the shed wake behind the airfoil is convected at a nonuniform velocity (see Fig. 8.25), and this causes several complications in the mathematical treatment of the induced velocity effects. Isaacs (1945,1946) derived a closed form solution for the additional unsteady aerodynamic effects of a harmonically varying free stream velocity. Greenberg (1947) published a similar theory, but made a high frequency assumption about the shed wake behind the airfoil to obtain a solution in terms of the Theodorsen function alone. An approximate theory for this problem was also developed by Kottapalli (1985), in which small “lead-lag” airfoil oscillation amplitudes with respect to the mean velocity were assumed. Johnson (1980) has also discussed the general problem of a varying velocity on unsteady airloads. Using the same assumptions made by Isaacs, complete expressions are given for the lift and pitching moment on an airfoil executing harmonic plunge and pitch motion about
![]()
|
|
|
|
|
|
|

 X = long
X = long
Figure 8.25 A time-varying free-stream velocity results in a nonuniform convection speed of the shed wake.
an arbitrary pitch axis. Essentially, Johnson’s conclusion is that the approximation using the Theodorsen function with the local reduced frequency is appropriate for flow oscillation amplitudes of up to 70% of the mean velocity. For small flow oscillation amplitudes, the Theodorsen function calculated with the reduced frequency argument based on the mean velocity will be accurate enough, which effectively means neglecting the unsteady free stream effects.
The theoretical problem of a time-varying free stream velocity on the unsteady aerodynamic response has been examined by van der Wall & Leishman (1994), both from the classical frequency domain approach and also from the time domain. This work reemphasizes that one of the significant effects of an oscillating incident flow velocity is a nonuniform convection velocity of the shed wake vorticity behind the airfoil. Van der Wall & Leishman
(1994) compare and contrast five theories representing the effect of the unsteady incident velocity variations: Isaacs’s theory, Greenberg’s theory, Theodorsen’s theory combined with unsteady incident velocity, Kottapalli’s theory, and the Duhamel superposition with the Wagner function. They found that, strictly speaking, all of the theories represent the case of a fore-aft moving airfoil instead of an unsteady incident velocity; this latter case should be more correctly viewed as a propagating horizontal gust field. A helicopter rotor blade section in forward flight encounters both unsteady sectional velocity (the superposition of rotation and forward flight velocity components), but in addition there is a fore-aft motion through the blade lead-lag degree of freedom. However, it was found that in the range of reduced frequencies encountered by a helicopter blade, the results obtained from all the various theories are essentially equivalent. Therefore, the interpretation of an unsteady free stream as equivalent to fore-aft motion of the airfoil can be viewed as a good approximation for the helicopter case. All of the theories cited above lead to the same noncirculatory expressions, and all were found to reduce to Theodorsen’s theory (or equivalent) when the varying part of the incident flow oscillation amplitude becomes zero.
As mentioned previously, in the time domain the effect of a time-varying velocity in an incompressible flow can be modeled using Duhamel superposition with the Wagner function. Again, the appropriate apparent mass forces must be included in the solution, even though they will be small for the frequencies and amplitudes of the fluctuating velocity typically found on a helicopter. In this case
jrb /.. d(Va)
C, W = -[h + -4r – aba)
+ f )/а(0)ф(і) + J (j)(s – a)da) . (8.69)
The distance traveled through the flow is now proportional to the area under the velocity versus time curve as given by Eq. 8.4. Van der Wall & Leishman have compared results obtained with this time domain method with Isaac’s frequency domain results, where the agreement is essentially exact.
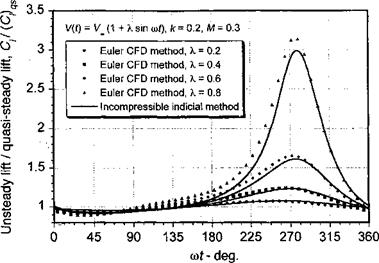
Results calculated using Eq. 8.69 are shown in Fig. 8.26 for the lift on an airfoil at a constant angle of attack, a, experiencing a harmonic oscillation of velocity of the form V(t) = Voo(l + A sin cot) at a reduced frequency, k, of 0.2 with A = 0, 0.2, 0.4, 0.6, and 0.8. The Duhamel integral was solved by means of a finite-difference approximation using the numerical scheme discussed in Section 8.14.1. The lift in Fig. 8.26 is shown as a fraction of the quasi-steady lift, (C[)qs = 2na. Also shown in this figure are results computed by means of a CFD method based on solutions to the Euler equations. It will be seen from Fig. 8.26 that at a given time the primary effect of unsteadiness is either an increase or attenuation
|
Figure 8.26 The effects of a nonsteady free-stream velocity on the unsteady lift for an airfoil with a constant angle of attack. (CFD calculations courtesy of Arun Jose.) |
of the unsteady lift compared to the quasi-steady result, which is a result already noted for oscillations in angle of attack. For 0°«wt <90°, the local velocity (and thus the product Va) is increasing. Here, the shed circulation has the opposite sign to the airfoil circulation and so the unsteady lift is less than the quasi-steady value. The higher local velocity here means that the shed wake is further away from the airfoil in a given time, and this effect contributes to a more rapid buildup in the circulatory lift compared to the case where the wake convection speed would be assumed uniform. For 90° <cot< 270°, the local velocity is decreasing. Here, the shed circulation has the same sign as the airfoil circulation, which tends to increase the lift over the quasi-steady value. Furthermore, for 180° < cot < 360° a velocity lower than the mean incident velocity means that the shed wake is closer to the airfoil; this then enhances the basic unsteady effect and the lift quickly becomes much greater than the quasi-steady values. Finally for 270° < cot < 360°, the local velocity is increasing again. With the change in sign of the wake circulation and the increasing wake convection velocity, the lift drops quickly to become close to the quasi-steady value again. Notice that in Fig. 8.26 there is good agreement between the incompressible theory and the CFD method,[32] despite the slight phase differences. Other theoretical work on modeling unsteady free stream velocity effects is given by Ashley et al. (1952) and Friedmann & Yuan (1977). The extension of this problem to subsonic compressible flow is not without its difficulties, but one approach is discussed later in Section 8.17.