Approximations to the Sharp-Edged Gust Functions

Mazelsky (1952a) and Mazelsky & Drishler (1952) have obtained exponential ap­proximations to the stationary sharp-edged vertical gust functions at various Mach numbers by means of reciprocal theorems in conjunction with numerical solutions for airloads com­puted in the frequency domain. A suitable functional approximation for the sharp-edged vertical gust is of the form

N

ir(s, Gie-8i (8.186)

;=i

where the Gi and gi coefficients will all be Mach number dependent, and with j Gі = 1

and gi, і = 1,…, N > 0. The corresponding lift is given by

(8.187)

It has been shown previously that the circulatory part of the total lift from a step change in AoA in subsonic compressible flow can be approximated by a two-term exponential func­tion, and for all subsonic Mach numbers the results are related through a characteristic time
that can be scaled in terms of Mach number alone. For later values of time the sharp-edged vertical gust and indicial AoA functions must approach each other; thus it is reasonable also to assume a similar behavior for the vertical gust function. It can be approximated by an exponential function of the form

N N

і £g, = i, gi> o,

i=l i=l but now the G s and gs are fixed and considered independent of Mach number. Like the

oi ЛлЛ _ __________ —_____ и~______ —и~

іиисаіиїла given рісуіииму, ьиеи an ajjpnjAimaiiuii eon uc аьмииси їй uc

valid up to at least the critical Mach number of the airfoil, beyond which nonlinear effects associated with transonic flow do not allow for such relatively simple generalizations.

The solution for the coefficients in Eq. 8.188 can now be formulated as a least-squares optimization problem with several imposed constraints. In this case, however, there are no equivalent experimental results for airfoils in sinusoidal gust fields. Therefore, direct time domain results obtained using analytic and CFD solutions can be used as a reference to find the gust function approximations in exponential form. To obtain an approximation to the exact linear theory, one constraint can be imposed by matching the time rate of change of the exact solution (Eq. 8.183) and approximate solution (Eq. 8.187) at s = 0. This helps constrain the solution to ensure that the exact result will always be closely obtained in the initial stages. This part of the response is particularly important for transient aerodynamic phenomena such as BVI – see Section 8.16.4. Differentiating Eqs. 8.183 and 8.188 with respect to s and equating their gradients at s = 0 leads to a definition for the first constraint, namely

This result cannot be obtained over the entire subsonic Mach number regime; however, an evaluation of right-hand side of Eq. 8.189 shows that it is numerically close to 0.6 over the practical range 0.2 < M < 0.8. As M -»■ 0, the slope tends to infinity at s = 0, which is consistent with the exact solution given by von Karman & Sears (1938). In the latter case, with any common type of exponential approximation to the exact incompressible solution [see, for example, Bisplinghoff et al. (1955)] the gradients cannot be matched as s -* 0. In addition, a constraint is imposed for the initial conditions, namely Y^=i G, — 1 = 0, and also Gj, gi, > 0, і = 1, 2,…, N. Also, as 5 сю, the airloads approach the value given by the usual steady-state subsonic linearized airfoil theory [i. e., C„(s = оо, M) = 2п/ft]. In a parallel way to that described previously for the indicial AoA case, a 2A-dimensional vector of unknown coefficients can now be defined as

хГ = {Gi &2 • • • g g2… gw) •

The vector in Eq. 8.190 can be chosen to minimize the differences between the approxi­mating exponential vertical gust function and the exact or any reference solutions over the domain of s and M.

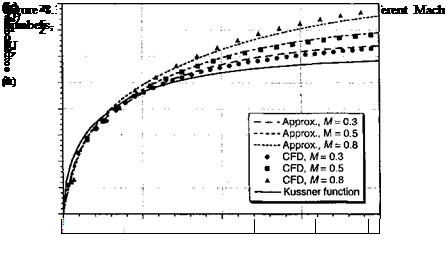
Exact results for the vertical gust response in linearized subsonic flow can be com­puted using the solutions given by Lomax (1968) and Lomax et al. (1952), but only up to s = 4M/(1 — M2). For higher Mach numbers this corresponds to finding an exact solution up to about 10 semi-chord lengths of airfoil travel. CFD results for the sharp-edged gust

20

problem have been made available by Singh & Baeder (1997b). Notice that the exponential approximations to the gust response, which are shown in Fig. 8.35, match the exact solutions and the CFD solutions almost precisely. It is apparent that although the final values increase with increasing Mach number, the initial growth in lift is less.

The resulting coefficients for the indicial gust functions are given in Table 8.3. Results for the N = 3 case at M = 0.5 as given by Mazelsky & Drischler (1952) are also tabulated. The coefficients of the generalized subsonic vertical gust function as M 0 are close to those given by R. T. Jones (1938,1940) for the incompressible case (the N = 2 exponential approximation to the Kussner function) and confirms that the results for the subsonic case are closely approximated by scaling the g coefficients by /32; that is, the aerodynamic vertical gust responses are related in subsonic flow, albeit approximately, through a characteristic time.