Blade-Vortex Interaction (BVI) Problem
Blade-vortex interaction (BVI) is one practical example of a helicopter flow with an intense vertical velocity field with high velocity gradients. The 2-D BVI problem, which is shown schematically in Fig. 8.36, has been widely addressed in the literature – see, for example, McCroskey & Goorjian (1983) and Singh & Baeder (1997b). While passing an airfoil at a predetermined distance, a convecting vortex of positive circulation produces a downwash velocity while upstream of the blade (airfoil), and this changes to an upwash as it moves downstream. This situation leads to a rapidly and continuously changing angle of attack, resulting in highly unsteady aerodynamic lift and other airloads. The acoustic pressure (or noise) propagated to an observer from such a blade-vortex encounter is related, as given by the compact source limit, to the time rate of change of this lift (see Section 8.19).
Representative numerical calculations will now be shown for the unsteady loads on a NACA 0012 airfoil interacting with a convecting vortex of nondimensional strength Г = Г/(Ус) = 0.2. The airfoil is assumed to have zero angle of attack. The interacting vortex was assumed to have a Lamb-like normal velocity distribution (see Eq. 10.9) given
![]() (8.197)
(8.197)
with r2 = (x — xv)2 – f (y — yv)2, where xv, yv refer to the position of the vortex relative to a coordinate axis at the leading edge of the airfoil. The reciprocal influence of the airfoil on the vortex convection velocity and trajectory is neglected, and we can assume that the vortex remains undisturbed from the path yv = yQ = —0.26. As shown by Srinivasan& McCroskey
(1987) , the effect of vortex trajectory distortion appears to be of secondary importance to the overall airloads except for the transonic case when the vortex may pass close to a shock wave. A viscous core of dimensions rc = 0.05c was used for the calculations, although the interaction between the airfoil and the vortex is sufficiently spaced in this case that the core radius does not play a role.
|
|
|
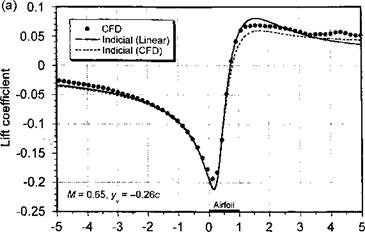
Vortex position, xv (chords) Figure 8.37 Comparison of indicial method with Euler CFD result for the lift during a 2-D vortex-airfoil interaction, f = 0.2 and y0 = —0.26. (a) M = 0.65 (subsonic), (b) M = 0.8 (weakly transonic). |
Results for Mach numbers between 0.65 and 0.8 are shown in Fig. 8.37. The results are compared to a CFD solution based on the Euler equations. Notice the good agreement between the indicial approach and the CFD solution, the results essentially confirming the validity of linear theory for this problem. Even for the higher Mach number of 0.8, where some nonlinearities because of the transonic nature of the flow might be expected, the agreement is good, although there is a somewhat larger lift overshoot downstream of the airfoil trailing edge compared to that predicted by the Euler method. The results in Fig. 8.37 also indicate that that the peak-to-peak value of the lift response becomes attenuated with increasing Mach number, which is exactly the opposite to the result obtained using quasisteady, subsonic airfoil theory or incompressible unsteady airfoil theory. Also, it is apparent that the effects of increasing Mach number introduces a significantly larger phase lag in the lift response, which obviously becomes a critical consideration when accurate noise predictions are an issue (see also. Question 8.12).
|
|
|
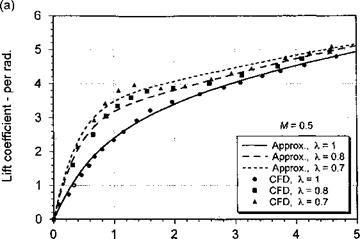
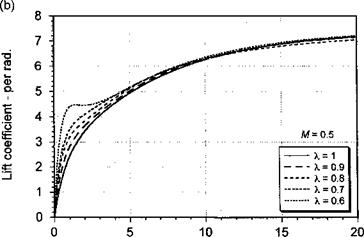
Distance traveled by airfoil in semi-chords, s Figure 8.38 Convecting sharp-edged vertical gust indicial lift functions for different gust speed ratios at M — 0.5. (a) Short values of time, (b) Longer values of time. |