Broadband Noise from Lifting Surfaces. Analytical Modeling and Experimental. Validation

Michel Roger

Ecole Centrale de Lyon

Abstract

The chapter is dedicated to the noise radiated by thin airfoils in either disturbed or homogeneous flows. This includes noise pro­duced by impingement of upstream turbulence onto a leading edge, self-noise caused by boundary-layer turbulence scattering at the trailing edge and noise due to the formation of a vortex street in the near wake. Analytical modeling is proposed in the frequency do­main, based on linearized theories of unsteady aerodynamics. The same mathematical background referred to as Schwarzschild’s tech­nique is used for all mechanisms in order that the predicted trends can be compared. In a first step the analysis is focused on the derivation of the induced lift fluctuations, acting as the sources of sound according to Ffowcs Williams & Hawkings’ analogy. The radiation properties of isolated aerodynamic wave-numbers in the sources are discussed in a second step. Next a statistical declination of the formalism is introduced, relating the source statistics to the PSD of the acoustic pressure in the far field. Finally the statistical models are assessed against experimental data.

1 Introduction

1.1 Methodology and Context

Rotating blades, wings with high-lift devices and other so-called lifting surfaces (splitter plates, spoilers…) embedded in a flow generate aerody­namic sound by various declinations of vortex dynamics. Some of them have been introduced in chapter 2. If random disturbances are carried from up­stream in the oncoming flow, they are rapidly distorted around the leading edge of the surface. This produces what is often called interaction or im­pingement noise. It is not intrinsic to the surface but rather characteristic of the incident flow, even though the surface shape may have a large influence

R. Camussi (Ed.), Noise Sources in Turbulent Shear Flows: Fundamentals and Applications, CISM International Centre for Mechanical Sciences, DOI 10.1007/978-3-7091-1458-2_5,

© CISM, Udine 2013

on the produced noise. In absence of oncoming disturbances, the surface generates its own vortex dynamics through the formation of boundary lay­ers or the onset of vortex shedding, because of the effect of viscosity. The associated acoustic signature is called self-noise because it is more intrin­sic to the incriminated surface. Most applications involve airfoil-like lifting surfaces, defined by their chord and span lengths and some cross-section de­sign. Interaction noise and self-noise include span-wise distributed sources concentrated at the leading edge or the trailing edge, and localized sources at span ends (tips of blades, flap side-edges of high-lift devices…).

In all cases the prediction of the broadband noise is made a considerable task by the random character of the flow. The corresponding mechanisms can be addressed either numerically or analytically. Typically a numerical approach, based on the recent know-how in Computational Aero-Acoustics for a direct simulation or based on hybrid techniques, can be understood as a demanding extension (more than just a special case) of Computational Fluid Dynamics. An analytical approach is conceptually different. It is dedicated to an isolated, previously identified mechanism and needs drastic simplifications and assumptions on the flow features and/or on the geome­try. The general equations are linearized and the initial problem is generally interpreted as a wave-scattering problem. This major difference makes both approaches different jobs and what can be expected from one or the other one cannot fit with the same ambitions. The numerical techniques are aimed at understanding the tiniest details of the sound generating mechanism and describing or reproducing it as accurately as possible. This is achieved at the price of heavy, time-consuming computations. Some of them are not tractable yet for the Reynolds and Mach numbers of interest, making the field still open for further progress. Conversely the analytical investigations are aimed at providing approximate but very fast and cheep results. The previously required recognition of a mechanism makes the solution clearly expressed as a function of the main parameters of the flow, thus the solution itself is easily used to get information on the scaling laws and the underlying physics. This is very useful for preliminary design in engineering context. Within the scope of hybrid approaches, an analytical prediction model can also be used to deduce the far-field sound by post-processing an already available simulation of the flow. It is clear that both approaches remain necessary in any case, and for the both of them significant improvements and new achievements are made every year in the community of aeroa – coustics. On the one hand, numerical techniques become more and more attractive and tractable. On the other hand, analytical techniques can still be extended and thus have not yet reached their limitations. The present chapter is dealing more specially with flows developing on airfoils placed

in either disturbed or clean streams. It is focused on analytical prediction methods and their experimental validation.

(a) (b) (c)

Figure 1. Top: large-scale unsteady fluid motions around bodies. (a): splitter plate in turbulence; (b): stalled airfoil, (c): vortex shedding behind a cylinder. Bottom: turbu­lent boundary layer upstream of an airfoil trailing-edge, as example of small-scale motion.

1.2 Importance of Characteristic Scales

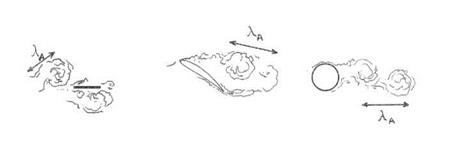
Whenever the dimensions of a solid body immersed in a disturbed flow are smaller than or of the same order of magnitude as some aerodynamic wavelength A a, the characteristic period of the experienced aerodynamic force variations on the body Aa/U0 is not small with respect to the travel­ing time of fluid particles over the body, say L/U0. In such conditions, the body responds as a whole to the disturbances, which can be defined as aero­dynamic compactness in the sense that the non-dimensional aerodynamic wavenumber 2 n /Aa is small. This also ensures that the body is acoustically compact because the acoustic wavelength A = Aa/M0 exceeds the body size, especially at low and moderate Mach numbers. Typical large-scale motions for which this asymptotic behavior makes sense are illustrated in Fig.1-top. They are the turbulence impingement on a flat body at low frequency (case (a)), the stall regime of an airfoil for which a large recirculating bubble forms (case (b)) and the shedding of vortices in the near wake of a cylinder (case (c)). In contrast the flow patterns of Fig. 1-bottom responsible for the emis­sion of trailing-edge noise correspond to much smaller scales which involve more subtle mechanisms. Typically for the narrow-band vortex-shedding sound of a cylinder in a flow, any cross-section of the cylinder is equivalent to a point dipole as stated in chapter 2. A relevant model based on the defi­nition of an unsteady lift coefficient has been proposed by Goldstein (1976). The same would hold for any bluff body, introducing adequate global aero­dynamic coefficients able to provide a description of the equivalent dipoles. A finer description in terms of distributed wall-pressure fluctuations will be needed for the configuration of Fig. 1-bottom, as shown later on.

In the present chapter the general framework introduced in Fig. 1 is reduced to span-wise distributed sources of broadband noise for relatively thin airfoils. Two mechanisms clearly dominate in most situations, namely interaction with upstream turbulence and boundary-layer turbulence scat­tering at the trailing-edge. The both of them are different declinations of the same basic process: sound is generated as the inertia of a vortical pat­tern is modified by its interaction with a singularity on a solid surface. The first mechanism, referred to as turbulence-impingement noise or leading – edge noise, involves the breakdown of oncoming vortices on the airfoil and, as such, corresponds to equivalent acoustic sources concentrated at the lead­ing edge (Fig. 1-d of chapter 2). Nevertheless the trailing edge is involved as well in the response of the airfoil, at least as far as the scales in the incident flow are not negligibly small when compared to the chord length. A basis for the modeling will be the use of unsteady aerodynamic theories presented in the next section. Trailing-edge noise involves a modification of the incident vortices due to the secondary vorticity shed in the wake as a consequence of the Kutta condition; the corresponding acoustic sources concentrate at the trailing edge. In each case, sound radiation is associated with a sudden change in the boundary conditions applied to convected vortical patterns. In the case of a blunted trailing edge or when the boundary layer thickness is small enough with respect to the physical trailing-edge thickness, von KArman vortex shedding takes place in the near wake, similar to case (c) of Fig. 1 but at smaller scale (Fig. 1-c of chapter 2). The shed vortices induce pressure fluctuations on the surface close to the trailing edge, again producing vortex-shedding sound. This mechanism is considered different from trailing-edge noise and will be addressed separately.

The general methodology described in the next sections relies first on linearized unsteady aerodynamic theories to get an approximate descrip­tion of the equivalent acoustic sources. Because the addressed mechanisms involve thin airfoils in subsonic Mach number flows, on the one hand, and because only non-accelerated motion is considered, the aerodynamic noise is essentially unsteady-loading noise. The noise itself is deduced in a second step using the acoustic analogy.