Determination of Indicial Function Coefficients
The coefficients A, A2, b, and bj are used to define the intermediate behavior of the indicial lift approximations. Using experimental results for the total lift and pitching moment response resulting from a prescribed harmonic forcing, such as oscillations in pitch or plunge, we can relate these data back to empirically determine the coefficients of the indicial functions. Experimental data are available from a number of sources. For the most part, they comprise measurements of the unsteady aerodynamic lift and pitching moment as a function of reduced frequency from pitch and plunge oscillations performed under nominally attached flow conditions; that is, in the region where linearized aerodynamics are appropriate. It is essential that the data selected be for attached flow conditions as the presence of nonlinearities that arise from flow separation effects introduces further complications in the validation of the indicial responses. In Beddoes (1984) and Leishman (1993), data were taken mainly from the results of Liiva et al. (1968), Wood (1979), and Davis & Malcolm (1980).
Because the indicial functions have been completely defined as exponential functions of time, they may be easily manipulated using Laplace transforms. If we consider just the
circulatory part of the lift from AoA given by Eqs. 8.131 and 8.134, the Laplace transform of this part of the indicial response function yields
|
2Vbf2 2 Vb2f2 The Laplace trar of attack) is given by a(p) = 1/p. The circulatory lift transfer function can be simplified to A A2 |
where
Because the initial value of the circulatory indicial response is zero (i. e., фс{0, M) = 0), then (1-А! — A2) = 0 and the lift transfer function simplifies further to
For the noncirculatory lift from angle of attack, the Laplace transform of the indicial response yields the transfer function
![]() C"c(P) _ 4 / 7> a(p) M 1 + Цр
C"c(P) _ 4 / 7> a(p) M 1 + Цр
|
Ab2p4 A2b2p4 4 / 4ic2M2k2 ‘ bf4 + k2 + blP4 + k2) + M +4к2М2к2 ‘ Афф2к A2b2p2k 4 / 2KaMk b2p4 + k2 + bp4 + k2) + M Vl+4KaM2k2 |
|
/ AbP2k2 ( Afi4k |
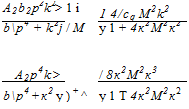 |
||
and the transfer functions for the other lift components can be derived in a similar way. Therefore, for any forcing function for which a Laplace transform may be easily derived (such as for a sinusoid), the lift and pitching moment response may be derived in explicit form by using inverse Laplace transforms in terms of the assumed form of the indicial response function (see also Questions 8.4-8.7). For example, the lift response to a harmonic pitch oscillation with a reduced frequency к about the 1 /4-chord axis of the airfoil may be obtained after some algebra as
where [Я and S3 denote the real and imaginary parts of the aerodynamic response, respectively. The resultant frequency response can be obtained by summing the various contributions to the real and imaginary components. A similar approach can be adopted to find the response
|
Table 8.2. Coefficients of Indicial Lift Approximation Deduced from Oscillating Airfoil Experiments
|
from harmonic plunge oscillations, which of course, are useful because they do not include any pitch rate (q) terms in the aerodynamic response.
A vector x can now be defined that consists of the coefficients At, A2, by, and b2 used in the indicial lift function:
xr = (A, A2;b, Ьг-, &„,&„)■ (8.150)
The additional factors 8a and 8q are empirical values chosen to modify the initial value of the indicial response functions to account for the possibilities of 3-D or finite-span effects present in the airfoil measurements. It has been shown, however, that their values are always close to unity, suggesting that the unsteady airfoil measurements selected are indeed representative of 2-D unsteady flow. The vector in Eq. 8.150 must be chosen to minimize the difference between the explicit solution based on the assumed indicial response approximations and the reference solutions (in this case, experimental results) for the unsteady lift in the frequency domain. If the real and imaginary parts, Fm(M, ) and Gm(A/, ), respectively, are known at up to M values of reduced frequency and at each of I values of Mach number, an objective function J(x) can be defined as
/
J = ]Tj(x, Mi), (8.151)
/=i
where
M
J(x, Mi) = [Fm(Mi) – ЯС„(х, Mi, km)]2 + [Gm(Mi) – 3C„(x, Mt, km)f .
m= 1
(8.152)
The minimum of the objective function J in the parameter space x will give the best approximation to the known (reference) lift transfer function. Therefore, the objective function minimization algorithm is basically a nonlinear programming problem of minimizing J(x) subject to the constraints
2
An, bn > 0, n = 1,2 and 0 < 8a, 8q < 1 and An = 1. (8.153)
n=l
The latter equality constraint may be replaced by a penalty function. Notice that although Table 8.2 shows that the different sets of experimental data result in slightly different values of the coefficients A, A2, by, and &2, the differences are of limited practical significance; the quality of the derived indicial functions is as good as the quality of the experimental data.











