Dispersive Waves of Physical Systems

Many physical systems support dispersive waves. Examples of commonly encoun­tered dispersive waves are small-amplitude water waves, waves in stratified fluid, elastic waves, and magnetohydrodynamic waves. A common feature of these dis­persive waves is that they are governed by linear partial differential equations with constant coefficients. The following are some of these equations.

a.

Klein-Gordon equation

b. Beam equation

д2ф + 2 д4ф = 0 W + p 9X4 = °-

c. Linearized Korteweg de Vries equation for water waves

дф д 3ф

~dt + p~X “ 0

d. Linearized Boussinesq equation for water and elastic waves

Э2ф _ 2 дф _ 2 д4ф = 0 dt2 а дх2 ^ дХ2дt2

Because these equations are linear with constant coefficients, they can be read­ily solved by Fourier-Laplace transform. The Fourier-Laplace transforms of these equations are

(a) (of2 _ (fa2 _ p2)ф = H1 (а, ш).

(b) (of2 _ p2a4)ф = H2(а, ш).

(c) (ш + pa3)ф = H3(a).

(d) (ш2 _ (fa2 + p2a2of2)ф = H4(а, ш).

The right-hand side of each of these equations represents some arbitrary initial conditions. The bracket multiplying the transform of the unknown on the left side of each equation is called the dispersion function, which will be denoted by D(a, m). The dispersion relation of the dispersive waves is given by the zeros of the dispersion function; i. e.,

D(a, m) = 0 ^ ш = ш(а).

Eq. (4.1) is a relationship between wave number a and angular frequency ш.

The solution of a dispersive wave system in wave number space, in general, may be written in the following form:

H(а, ш)

и =————-

D(a, ш)

The corresponding solution in physical space is found by inverting the transforms of Eq. (4.2) as follows:

и(х, t)	(4.3)

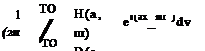Suppose, for real a, the dispersion relation has a simple real zero. That is, ш(а) is a solution of

D(a, ш(а)) = 0.

Thus, for the ш-integral of Eq. (4.3), there is a pole lying on real ш-axis. The contribu­tion of this pole can be found by evaluating the ш-integral by the Residue Theorem. This gives, t > 0

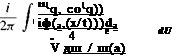и(х, t)

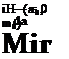where Ф = a(x/t) — m(a) is the phase function of the integral. For large t, Eq. (4.5) may be evaluated asymptotically by the method of stationary phase (see Appendix B). The stationary phase point as is given by

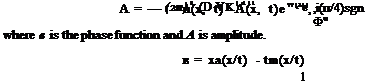Subscript s indicates the evaluation at a = as(x/t). In the following, the subscript s is dropped with the understanding that a is as(x/t) and m is m(as). The asymptotic formula may be rewritten in the compact form as follows: