DUTCH ROLL MODE

A physical model that gives an approximation to the lateral oscillation is a “flat” yawing/sideslipping motion in which rolling is suppressed. The corresponding equa­tions are obtained from (4.9,19) by setting p = ф = 0 and dropping the second (rolling moment) equation. The term in Yr is also neglected in the first equation. The
result is

V = fyvV — u0r r = Nvv + Nrr

The corresponding characteristic equation is readily found to be

A2 – (% + Mr)A + ($ljrr + u0Nv) = 0 (6.8,12)

The result obtained from (6.8,12) for our example is XnR = —0.1008 ± 0.9157г, or

T = 6.86 sec

AU= 1.0

The approximation for the period is seen to be useful (an error of about 3%) but the damping is very much overestimated.

There is another approximation available for the damping in this mode that may give a better answer. It follows from the fact that the coefficient of the next-to-highest power of A in the characteristic equation is the “sum of the dampings” (see Exercise 6.4). Thus it follows from the complete system matrix of (6.8,2) that

2 nDR + R + s = e9v + ^£p + Яг

or nDR = U°!)v + £p + Mr-(AR + A5)} (6.8,13)

But the approximation (6.8,11) for the roll and spiral modes gives precisely

_ D

On using (6.8,11) we get the expression

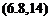l S

+ Nr + — Iff———-

К Щ

which is to be compared with + Яг) given by (6.8,12). The damping obtained from (6.8,14) is nDR = —0.0159, better than that obtained from (6.8,12) but still quite far from the true value of —0.0330. The simple average of the two preceeding ap­proximations for the Dutch Roll damping has also been used. In this instance it gives nDR = —0.0584, which although better is still 77% off the true value.

This example of an attempt to get an approximation to the Dutch Roll damping illustrates the difficulty of doing so. Although the approximation tends to be better at low values of CL, nevertheless it is clear that it must be used with caution, and that only the full system matrix can be relied on to give the correct answer.