EFFECT OF CG LOCATION

It was indicated in Chap. 2 that the single most important aerodynamic characteristic for longitudinal stability is the pitch stiffness Cma, and that it varies strongly with the CG position, that is,

cma = cLa(h – hn)

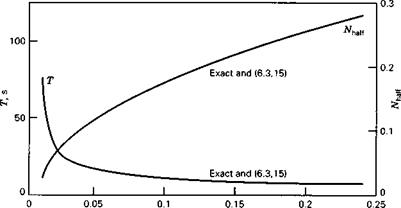
where the static margin is Kn = hn — h. The effect of this parameter is demonstrated by using (4.9,18) with variable Kn. The results, with all the other numerical data iden­tical with that in Sec. 6.2, are shown in Figs. 6.7-6.9. Figure 6.7 shows that the phugoid period and damping vary rapidly at low static margin and that the approxi­mation (6.3,10) is useful mainly at large Kn. Figure 6.8 shows the variation of the

(с)

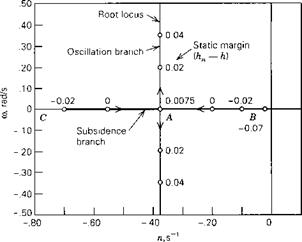
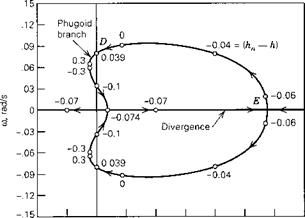
Figure 6.9 (а) Locus of short-period roots, varying static margin, (b) Locus of phugoid roots,

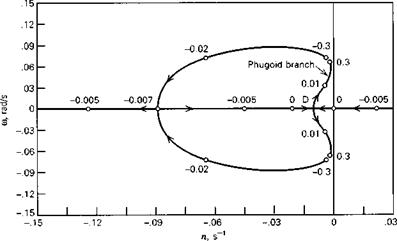
varying static margin, (c) Locus of phugoid roots, varying static margin, Mu = 0.

short-period roots. These, too, vary strongly with pitch stiffness, the mode becoming nonoscillatory at a static margin near zero. The approximation (6.3,15) is excellent over the whole oscillatory range.

Important additional insight into these modes is obtained by examining the root loci obtained by varying the static margin. These are shown in Fig. 6.9. Figure 6.9a shows that the damping, n, of the short-period mode remains virtually constant with decreasing Kn while the frequency, to, decreases to zero at point A where the locus splits into two real roots, branches AB and AC of the locus. These of course represent nonperiodic modes or subsidences. Figure 6.9b displays the much more complex be­havior of the phugoid. With reducing static margin (rearward movement of the CG) this mode becomes unstable at point D. At (totally unrealistic!) negative static margin beyond —0.1, a new stable oscillation has reappeared. However, it is accompanied by a catastrophic positive real root far to the right.

The importance of the Mu derivative was shown earlier. It is again displayed in Fig. 6.9c, which repeats the locus of the phugoid roots with Mu set equal to zero. The corresponding locus for the short-period roots is almost identical to Fig. 6.9a. The pattern with Mu = 0 would be more representative of a rigid airplane at low Mach number. It shows a stable phugoid at all static margins as Kn is decreased until it splits at point D into a pair of real roots. The left branch from D then interacts with the branch AB of the short-period locus to generate a new stable oscillation while the right branch crosses the axis to give an unstable divergence at negative static margin.