Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
EFFECT OF SPEED AND ALTITUDE
Even for the “basic” case of a rigid airplane at low Mach number, the variation of the lateral modes with speed and altitude may not be simple. This is because some of the lateral stability derivatives are dependent on the lift coefficient in complex ways. That is especially true of airplanes with swept wings and low aspect ratio for which Clfj increases markedly with CL. These effects will appear most strongly at low speed and high altitude, both of which require high CL. (Note that in the B747 example at M =
0. 8 and 40,000 ft, CL = 0.654, which is quite large for cruising flight.) For a rigid swept-wing airplane at low Mach number the period of the Dutch Roll mode would be expected first to increase and then to decrease as the airplane speed increases. The damping of this mode would be expected to be weak at low speed and to increase at higher speeds. The rolling convergence is well damped at all speeds, but the damping would normally increase with speed. The spiral mode is frequently unstable over some portion of the speed/altitude flight envelope, depending on the interplay of the derivatives that appear in (6.8,6). The characteristic times of this mode are, however, usually so long that the instability does not degrade the handling qualities unduly.
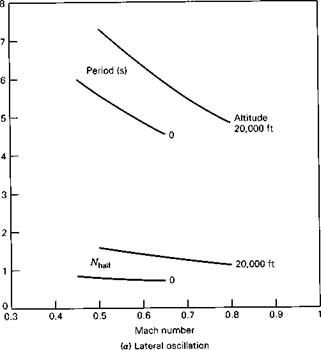
The effect of increasing altitude at fixed CL is primarily an increase in the damping time constants of all the modes. The period of the Dutch Roll is not much affected.
When substantial aeroelastic and compressibility effects are added to the already complex behavior of the lateral modes, the result is an even more irregular pattern of modal characteristics. The data of (Heffley and Jewel, 1972) for the B747, reproduced in Table 6.10 show this. (Note that a negative fh. l!f implies an unstable mode.) At the two lower altitudes, with relatively low values of CL, the modes are seen to behave in a fairly regular way (see Fig. 6.16). However, at 40,000 ft and high Mach
|
Table 6.10 Variation of Lateral Modes with Speed and Altitude
|
|
|
|
|
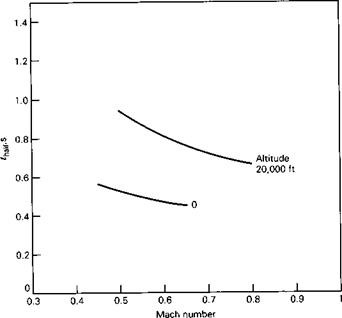
(b) Rolling convergence
Figure 6.16 Variation of lateral modes with speed and altitude, (a) Lateral oscillation, (b) Rolling convergence, (c) Spiral mode.
|
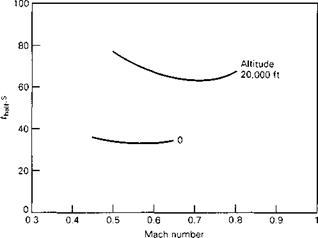
(c) Spiral mode Figure 6.16 (Continued) |
number the lateral behavior is quite irregular, especially the variation of the damping of all the modes with M. The spiral mode is seen to be unstable (albeit with long time constant) at both M = 0.7 and 0.9 but stable at M = 0.8. This behavior is primarily the result of the complex variation of C, with CL and M in this region.
