Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Error Propagation, Sensitivity and Total Uncertainty
According to the general uncertainty analysis formalism (Ronen 1988; Bevington and Robinson 1992), the total uncertainty of pressure p is described by the error propagation equation
 |
 |
 |
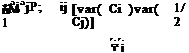where ptj = cov(CiCj)/[var( Ct)var( Ci)]1/2 is the correlation coefficient between the variables Ct and Ci, var(Ct) = < ACt2 > and
cov(Ci C j) = < ACi AC j > are the variance and covariance, respectively, and the notation < > denotes the statistical ensemble average. Here, the variables (Cj, i = 1–M} denote a set of the parameters Dt(At), Dx(Ax), Dq0(At), V,
Vref, nc/ncref, Пf/nfref, h/href> c/cref, q0/q0ref, pref, T, A and B in Eq.
(7.2) . The sensitivity coefficients St are defined as St = ( C/p )( dp/dCt ). Eq.
(7.3) becomes particularly simple when the cross-correlation coefficients between the variables vanish (ptj = 0, i Ф j).
Table 7.1 lists the sensitivity coefficients, the elemental errors and their physical origins. Many sensitivity coefficients are proportional to a factor (p = 1 + [A(T)/B(T)] /(p/pref ). For Bath Ruth + silica-gel in GE RTV 118,
Figure 7.1 shows the factor 1 + [A(T)/B(T)]/(p/pref ) as a function of p/pref for different temperatures, which is only slightly changed by temperature. The temperature sensitivity coefficient is ST = – T[B’ (T) + A'(T) pref/p]/B(T ), where the prime denotes differentiation respect with temperature. Figure 7.2 shows the absolute value of ST as a function of p/pref at different temperatures.
After the elemental errors in Table 7.1 are evaluated, the total uncertainty in pressure can be readily calculated using Eq. (7.3). The major elemental error sources are discussed below.
|
Table 7.1. Sensitivity coefficients, elemental errors, |
and total uncertainty of PSP |
|||
|
Variable |
Sensi. |
Elemental Variance |
Physical Origin |
|
|
£ |
Coef. s |
var( C t) |
||
|
1 |
Dt(At) |
f |
[(dV/ dt)( At)/V]2 |
Temporal variation in luminescence due to photodegradation and surface contamination |
|
2 |
DJAx ) |
(p |
[ (dV/dx)2 a2 + (dV/д y )2 a 2y]V ~2 |
Image registration errors for correcting luminescence variation due to model motion |
|
3 |
Dq0(At) |
(p |
[( дqo / д t)( At)/qoref]2 |
Temporal variation in illumination |
|
4 |
Vef |
(p |
Vref ghv Bd |
Photodetector noise |
|
5 |
V |
– <p |
VGhv Bd |
Photodetector noise |
|
6 |
n cmCf |
<p |
[Ry/(Ri + Ry )]y(ARi/Ri )y |
Change in camera performance parameters due to model motion |
|
7 |
П f/П fref |
(p |
var(nf/Пfref ) |
Illumination spectral variability and filter spectral leakage |
|
8 |
h/href |
(p |
[ (h/дx)y aX + (h/дy)2 ay ] h-f |
Image registration errors for correcting thickness variation due to model motion |
|
9 |
c/cref |
(p |
[(дє/dxf aX + (де/дy) aj ] c~ry |
Image registration errors for correcting concentration variation due to model motion |
|
10 |
q 0 /q 0 ref |
(p |
(qorffy( Vqo) •( AX )f |
Illumination variation on model surface due to model motion |
|
11 |
Pref |
1 |
var( p) |
Error in measurement of reference pressure |
|
12 |
T |
st |
var( T) |
Temperature effect of PSP |
|
13 |
A |
1 – (p |
var( A) |
Paint calibration error |
|
14 |
B |
-1 |
var( B) |
Paint calibration error |
|
15 |
Pressure mapping |
1 |
(д p/дх) ay + (p/ду )y a X |
Errors in camera calibration and pressure mapping on a surface of a |
|
and |( V pLf •(AX if |
presumed rigid body |
|||
|
Total Uncertainty in Pressure var(p)/ p2 |
= £ Siyvar( Ct)/ CІ i = 1 |
Note:
(1) <7x and <ry are the standard deviations of least-squares estimation in the image registration or camera calibration.
(2) The factors for the sensitivity coefficient are defined as <p = 1 + [ A(T)/B(T)](pref / p) and St = -[T/B(T)][B'(T) + A'(T)(p„f/p)] .
 |
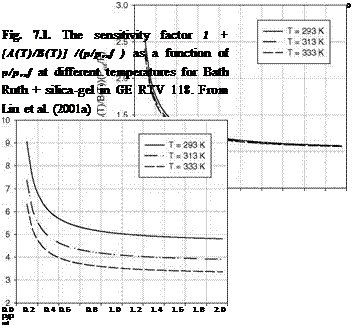Fig. 7.2. The temperature sensitivity coefficient as a function of p/pref at different temperatures for Bath Ruth + silica-gel in GE RTV 118. From Liu et al. (2001a)
