Formulation of the Full and Reduced Problems in Terms of Stream Functions

For steady two dimensional and axisymmetric compressible flows as well as for unsteady one dimensional flows, a stream function can be introduced to satisfy the continuity equation identically.

For example, in 2-D case, using Cartesian coordinates, one can use

дф дф

pu = , and pv = —-

dy dx

The equation for ф is given by

where w is the vorticity.

The equation for w, for steady isoenergetic flow is given by Crocco equation

(12.81)

or, simply w/p is constant along a streamline. The vorticity is related to the entropy gradient

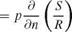(12.82)

where n is normal to the streamline. Notice S is constant along a streamline but it jumps across a shock.

Hence, the application of such a formulation requires the identification of the shock shape and position to find the jump of entropy.

There is another problem, even for irrotational flow, the density is not a single valued function of the mass flux. Indeed, for a given flux, there are two values, one for subsonic and the other for supersonic conditions. This is obvious considering the compressible flow in a stream tube (or a nozzle). Moreover, there is a square root singularity at the sonic point. The density is not defined (imaginary) for flux values higher than the sonic flux. The stream function equation is, in general, of mixed type as can be easily shown from the equivalent non-conservative form

u2 д2ф uv д2ф v2 d2 ф 22 ( 1 2 d ( S

— a2 dx2 — 2 a2 dxdy + 1 — a2 dy2 =~— a Y—1 + M° Лф Cp

where a is the speed of sound given by Bernoulli’s law

There is another form of the stream function equation introduced by Crocco, where the derivatives of ф is determined by the velocity component u and v only.

Let

(12.85)

effects is given by

Pai found analytical solution for attached shocks to a plane ogive. He also found analytical solution to the axially symmetric case. He concluded that the first order linearized theory failed at certain points in the weak shock region and he suggested to use the method of characteristics to solve the full equations in the neighborhood of these points.

On the other hand, Kogan [50] obtained solutions for Crocco’s stream function equations for both two dimensional and axisymmetric flows with shocks attached to the leading edges. His results for biconvex parabolic airfoil are in good agreement with the method of characteristics near the airfoil leading edge. using successive approximation, taking the flow behind a plane shock wave as zero-order, the shock wave profile obtained in each step is used to determine the domain and the boundary conditions of the next step.

For axially symmetric flow, the flow past a cone is used a zero-order approxima­tion for the ogive problem. Successive approximations with appropriate boundary conditions are solved analytically. The first order solution for V contains a |-power branch point at в = в0 (the cone surface) and no logarithmic term as reported by Shen and Lin [51]. Shen and Lin results seem to give infinite pressure gradient at the ogive surface, although solutions by the method of characteristics give no such indication.

The stream function formulation for the reduced problem was used by Van Dyke in his hypersonic small disturbance theory.

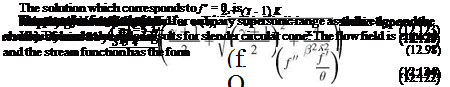and boundary conditions

The tangency condition at the surface of the cone is f (b) = 0.

Van Dyke solved the nonlinear ordinary differential equation for f numerically, step by step, starting from the shock surface inward until f vanishes to produce the solution at the solid surface. The pressure coefficient is given by

(12.106)

The surface pressure agrees well with the results of the full equations (with error O (52) as expected).

Van Dyke calculated also the flow over plane ogive and ogive of revolution. Again, his results agree with Kogan’s.