General Spanwise Circulation Distribution

A more general solution for the spanwise circulation Г(у) in Eq. (8.16) can be obtained by describing the unknown distribution in terms of a trigonometric expansion. Using the spanwise coordinate в, as defined in Eq. (8.23), the following Fourier expansion is selected:

The shapes of the first three symmetric terms in this expansion are shown schematically in Fig. 8.13, and all terms fulfill Eq. (8.17) at the wing tips:

Г(0) = Г(л) = 0

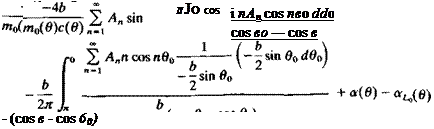Substituting Г(0) and dT(0)/dy into Eq. (8.16) yields

FIGURE 8.13

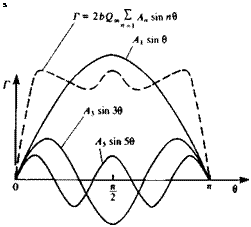Sine series representation of symmetric spanwise circulation distribution Г(0), n = l, 3. 5,….

By using Glauert’s integral (Eq. (5.22)) for the second term, this equation becomes

I, A• sin"e~ I, nA – s^j+a(e)~aUe)=0 (8’4*,)

Comparing this result with Eq. (8.16) indicates that the first term is – ae and the second term is —at:

Therefore the section lift and drag coefficients can be readily obtained:

рЄооГ(в) 4 b

Cdl = C, a, = —— 2 A„ sin пв( 2 kAk S‘~- —) (8.47)

c(tf) „ = i ч=і sin в /

-Ы2 S fba Cd(y)c(y) dy 2b2 Г ~ “ D, = —’—^——– = -^r 2 2 kAkAn sin кв sin nddd (8.49) J-b/2 О О J0 л — 1 * = 1

The wing aerodynamic coefficients are obtained by the spanwise integra­tion of these section coefficients:

for n Ф к я/2 for n = к

and for the lift integral only the first term will appear. The lift coefficient becomes

jzb2A

CL = ——^ = jryRAj (8.51)

•З

For the drag, only the terms where n = к will be left:

jib2 °° °°

CD. = — 2 nA2n = лЖ 2 пА2„ (8.52)

^ Л=1 Л = 1

By using the results for the lift, this can be rewritten as

where <5і includes the higher-order terms for n = 2, 3, . . . (only the odd terms are considered for symmetric load distribution). This clearly indicates that for a given wing aspect ratio, the elliptic wing will have the lowest drag coefficient since <5i > 0 and 6, = 0 for the elliptic wing.

Similarly, the lift coefficient for the general spanwise loading can be formulated as

CL = лЖАх = m(ar – au)

Assume that the wing is untwisted and therefore a – aL0 = const. Following Glauert (Ref. 5.2, p. 142) we define an equivalent two-dimensional wing that has the same lift coefficient CL. This wing is now set at an angle of attack or* — aL{) such that

CL = 2л(а* — ar^) (8.55)

The difference between these two cases is due to the wake-induced angle of attack, which is obtained from these two equations

(a – aj – <«* – aj – CL[±- T] . Sl <1 + ад (8.56)

and

1 +

where 62>0. Taking Al from this relation and substituting into Eq. (8.51) results in

2л(а – azj
!+ —(! + 52)

Thus, for the elliptic wing 62 = 0 and also its lift coefficient is higher than for wings with other spanwise load distributions.