Indicial Method for Subsonic Compressible Flow

All rotor aerodynamic problems involve compressibility to some degree. However, for subsonic compressible flow there is no analytic equivalent to Theodorsen’s theory, nor to the Wagner or Kiissner functions. This is because of the nature of the governing equation, which for the subsonic case is the hyperbolic wave equation versus the elliptic Laplace’s equation for incompressible flow [see Karamacheti (1966) and Chapter 14]. Therefore, alternative numerical means of finding the indicial responses must be derived. Because a time domain representation of the unsteady aerodynamics is sought, it is convenient to address the subsonic problem starting from the indicial response. Although this is by no means the only basis from which the problem can be tackled, it has already been shown that the indicial approach gives considerable physical insight into the problem of unsteady aerodynamics.

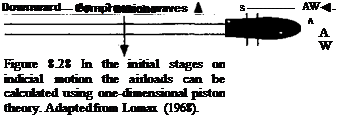
For a compressible flow, the initial loading on the airfoil after an indicial (step) input comprises a pressure wave system with a compression wave on one surface of the airfoil and an expansion wave on the other. This initial pressure loading on the surface can be computed directly using linear piston theory, which is a local wave equation solution for the unsteady airloads [see Lomax (1968)]. The piston theory gives a result valid for any Mach number, M, but only at the instant after the perturbation has been applied (i. e., at t = 0 or s — 0). If we consider a small element of an airfoil subject to a downward plunging type motion that produces a change in normal velocity Aw as shown in Fig. 8.28, then piston

theoi у gives the difference in pressure across the surface as Ap = 2,pa A. w, so

2paAw(x) f 4 ^ Aw(x)

= Pv2 = J V

Consider now a thin-airfoil undergoing a simultaneous plunging and pitching about the 1/4-chord. Figure 8.5 has shown that the normal velocity on the airfoil is composed of two primary modes: a uniform perturbation in w from the pure AoA contribution plus another uniform perturbation resulting from plunge velocity, h/V, and another perturbation mode

from the pure pitch rate of the airfoil q (= ac/V). By convention it will be assumed that the pitching motion takes place about the 1 /4-chord, although the result can be generalized to any pitch axis. For a step change in each mode, applying piston theory and integrating across the chord gives the normal force coefficients[33] at t = 0 as

ДСИа(0)= ^Act and ACnq(0)=^Aq (8.115)

and the initial moment coefficients about the 1 /4-chord as 1 7

AcmeW=- —Да ana ACm,(0) = —(8.116)

For subsequent time, pressure waves from the airfoil propagate at the local speed of sound and, in the absence of any other forcing, the loading will decay rapidly with time from these initial “noncirculatory” values. For a compressible flow the noncirculatory terms do not appear as an infinite pulse at s = 0 as for incompressible flow, but are finite in magnitude and decay more slowly from their initial values. Therefore, it will be appreciated that noncirculatory terms can no longer be assumed proportional to the instantaneous blade motion (i. e., to a, a, h) as they are for the incompressible case and, like the circulatory terms, they must also depend on the time history of the forcing. Physically this is because for an incompressible flow the pressure waves are propagated at infinite velocity, whereas for a real flow the disturbances propagate at the speed of sound.

Such a transient behavior is difficult to compute in subsonic flow, but some analytic solutions can be obtained for limited values of time after the step input has been applied. Using an analogy of unsteady 2-D subsonic flow with steady supersonic flow, solutions to the wave equation have been evaluated exactly by Lomax et al. (1952) to obtain the chordwise pressure loading on the airfoil in the short period in the range between 0 < s < 2M/(M+1). For a unit step change in AoA then

where the domain is x’ = x — Mt. This equation is valid for the early period 0 < t < c/(l + M). The symbol 9t refers to the real part where the real parts of the arc cosine of numbers greater than 1 and less than 1 are 0 and 7Г, respectively. Results are shown in Fig. 8.29 for M = 0.5. Notice the nature of the chordwise pressure loading as the upstream and downstream moving waves pass over the chord of the airfoil. Even after a very short time, the growth in circulation has been established, but the final value steady state circulation is only obtained after a relatively long time. Stahara & Spreiter (1976) and Singh & Baeder (1997a) show numerical solutions to the same problem using CFD methods.

By integrating the exact chordwise pressure loading solution in Eq. 8.117, the lift (normal force) and pitching moment during the short period 0 < s < 2M/(1+M)canbedetermined analytically. The lift coefficient resulting from a step change in AoA is

Cna(s) 4 Г 1-М

——– = —– 1————— 5

a M 2M