Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Indicial Pitching Moment from Angle of Attack
|
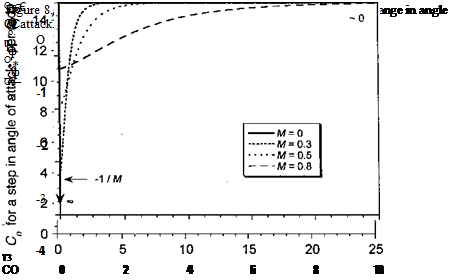
A similar process to that described previously can be used to find approximations for the other indicial response functions. The indicial pitching moment response about the 1 /4-chord resulting from a step change in angle of attack, a, can also be written as the sum of a noncirculatory part, , and a circulatory part, Ccma, that is, Cma(s) = C£(s, M) + Ccma(s, M) (8.154) or in terms of the indicial functions + у (°-25 – M) (8.155) For the noncirculatory part, a convenient general expression for the indicial function is of the form CM = Азехр + A4exp(^Oj. (8.156) One approximation to this function uses the values A3 = 1.5, A4 = —0.5, Ьз = 0.25, and = 0.1. Following a similar approach to that used above for the lift, but now using Eq. 8.155, gives the noncirculatory time constant as г“-=Шт«-= |
 |
Distance traveled by airfoil in semi-chords, s
Thus, the noncirculatory time constants Ta, TUm, Tq, and Tqm used in the indicial response functions are now defined in terms of the other (circulatory) coefficients. These functions are only weakly dependent on Mach number in the low subsonic flow regime; however, their values increase rapidly as M = 1 is approached but the theory breaks down here anyway.
The four basic indicial functions are plotted in Figs. 8.30 and 8.31 for several Mach numbers to illustrate their behavior. The considerable influence of Mach number compared to the incompressible values should be noted. In application, these subsonic indicial aerodynamic functions are manipulated in exactly the same way as that shown previously for the incompressible case when using the exponential approximation to the Wagner or Kussner functions. For example, in the case of the subsonic lift to an arbitrary variation in a, three recurrence equations or three states instead of two must now be used, with both the circulatory and the noncirculatory terms having a time-history effect.
