Nonuniform Vertical Velocity Fields

In the rotor plane, there are a large number of vortical disturbances that lie in proximity to the blades. This is especially significant on the advancing and retreating sides of the rotor where the blades may interact with tip vortices – see Section 8.16.4. The unsteady forces produced on a rotor blade arise primarily because of the vertical velocity between the wake disturbance (gust field) and the airfoil surface. In linear theory, this is treated as an imposed unsteady upwash field, which must be used to satisfy the boundary conditions of flow tangency on the airfoil surface. As described previously, within the assumptions of linear theory, incompressible flow solutions for the sinusoidal vertical gust problem have been solved by Sears (1940), and exact solutions for the sharp-edged vertical gust problem have been found by Kiissner (1935), von Karman & Sears (1938), and Miles (1956).

8.16.1 Exact Subsonic Linear Theory

For the subsonic compressible flow case, the problem of finding the sharp-edged vertical gust response, тf/(s, M), was considered by Lomax (1953) using a similar approach to that described previously to derive the indicial responses from changes in airfoil AoA and pitch rate. The subsonic vertical gust result was also obtained by Heaslet & Sprieter (1952) by means of reciprocal relations. The actual mathematical calculations are fairly involved, but Lomax (1953) has shown that exact analytical expressions for the airfoil pressure distribution can be found for a limited period of time after the vertical gust entry. For the period 0 < s < 2M/(1 + M) the lift coefficient is given by

(8.183)

for a gust velocity perturbation of Awg. me corresponding 1/4-chord pitching moment coefficient for the period 0 < s < 2M/(1 + M) can also be found, giving

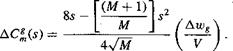(8.184)

Although these results are valid for less than one-chord length of airfoil travel for all subsonic Mach numbers, these analytic solutions are exact within the underlying assumptions of linearized, subsonic, unsteady thin-airfoil theory.

One interesting result from Eq. 8.183 is that increasing Mach number decreases the initial rate of lift production for a given distance traveled during the vertical gust penetration, perhaps not an intuitive result. However, a similar result has been shown previously for the indicial AoA case, where there is an increasing lag in the development of the circulatory lift for higher subsonic Mach numbers – see also Bisplinghoff et al. (1955). Using Eq. 8.183 it can be shown that the lift builds very rapidly during the vertical gust penetration, reaching close to one third of its final value (2 л ffi) shortly after the airfoil becomes fully immersed in the vertical gust (that is, when s = 2).

The position of the center of pressure during the vertical gust penetration is also of interest. Heiicoptef rotor blades tend to be relatively compliant in torsion compared to the wings of fixed-wing aircraft, and so the variation in airfoil pitching moment about the elastic axis can be very important. For the period 0 < s < 2M/(1 + M), the center of pressure can be computed from Eqs. 8.183 and 8.184 giving

which shows that xcp moves quickly aft to the 1/4-chord location within the short period 5 = 2M/(1 4- M). Therefore, for most practical purposes it is sufficient to assume that the aerodynamic center remains at the 1/4-chord throughout the vertical gust penetration. This result is also consistent with the incompressible solution of von Karman & Sears (1938). For later values of time up to s = 4M/(1 — M2), solutions for the airfoil pressure distribution during the vertical gust penetration takes a more complicated form, and the determination of the lift and pitching moment is only possible by means of numerical methods. For s > 4M/(1 — M2) no exact solutions to the sharp-edged vertical gust problem are possible in subsonic flow by means of the linear theory; consequently other and usually more approximate numerical methods or CFD solutions must be adopted.