Power Series Expansion of Pressure Coefficients

Dorrance [43] obtained analytical formulas for two-dimensional profiles via expand­ing the expression of the pressure coefficient as power series in K where the change of flow angle Лш is taken positive for compression and negative for expansion, hence for oblique shocks

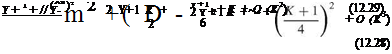For expansion fans, the expansion becomes

The first two terms of the two expressions are identical, the third terms differ slightly (-10%) for K = O(1).

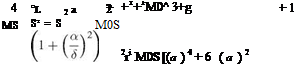Dorrance worked out in a manner like that of the linear Ackeret theory, simple forms for different profile shapes. For symmetric double wedge, the results are

12.2.3 Bodies of Revolution

The applicability of hypersonic similarity for cylindrical bodies with conical or ogival noses is demonstrated in Ref. [44]. For fitness ratio

F = length of the nose section/maximum diameter of the nose section (12.32)

the similarity parameter, K = M0/F

and for F > 2 and M0 > 2, the validity of the hypersonic similarity was estab­lished.

Hypersonic Flow over Cones

For large M0, the shock angle is close to the semi-vertex angle of the cone, в, hence

Cp = – L – – 1 = (Y + 1) в2 (12.33)

Y M2 -0

therefore

p – p0 – Y (Y + ^ K2 (12.34)

p0 2

with boundary condition

V. VB = 0, at B = 0

where B(x, y, z) = 0 represents the body shape.

The far field is uniform supersonic flow with M0 > 1. The shock wave is described by S(x, y, z) = 0 and it is not known.

The shock jump conditions can be obtained from the weak solution of the conser­vation laws. Conservation of tangential momentum requires that the velocity compo­nent tangent to the shock surface be continuous. The tangential velocity component is

Vt = (n л V) л n (12.42)

where n is the unit vector normal to the surface S, and

< u > < v > < w >

dS = dS = dS ’ at S =0

dx dy dz

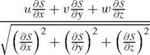The component normal to the shock is

and the other jump conditions at S = 0 are

dS dS dS

< pu > + < pv > + < pw > = 0

dx dy dz

The second law of thermodynamics requires that entropy does not decrease across shock waves, hence

< — >> 0, at S = 0 (12.48)

pY

The body is assumed to be thin where the streamwise slope of its surface is everywhere small compared to unity. A small parameter т is introduced which may be the thickness ratio or the angle of attack for inclined bodies.

From the tangency condition, all cross wind velocities are, in general, of order т. From the approximate solution for thin plane wedge, the pressure coefficient and the streamwise velocity perturbation are of order т2.

Such considerations suggest introducing new independent and dependent vari­ables as follows

yz

X = x, y = -, Z = —, B = B(X, y, Z), S= S(X, y, z) (12.49)

тт

u = U ^1 + т2й^ , v = UtV, w = UтW, p = p0p, p = yM^p0т2p

(12.50)

The above new quantities are dimensionless and of order unity for a body of unit length. The reduced first order equations in т are

(12.51) (12.52)

d p d y	(12.53) (12.54) (12.55) (12.56) (12.57) (12.58) (12.59) (12.53) (12.61) (12.62) (12.63)
dpv + dpv2 + dpvw
dx dy	d z
dpw dpv w d pw2 dX + dy + dZ	d p d Z
dpH + dpv HI + dpw HI ^
d x	d y	d z
with boundary conditions
d B _ д В _ д В + v – + w = 0, at В = 0 dx dy dz
or
d p В + d pv В + d pw В ^
d x	d y	d z
and
as x ^ —<x
Notice,
, __ . 7 and H — + 2u + —2 + w2 , 2 y — 1 P 2
The jump conditions at the shock wave become
dS dS dS < V > + < Pv > + < Vw > = 0 dx dy dv

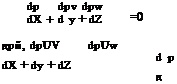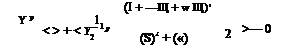(12.64)

Notice also, that the parameters M0 and т of the full problem appear only in the upstream condition on p, and not anywhere else, in the combination M0t.

Based on the above formulation, ignoring all т2 terms, the hypersonic similarity is justified.

It is interesting to notice that the error of first order small disturbance theories are of O (т2/3), O (t) and O (t2) for transonic, linearized supersonic and hypersonic flows respectively. A second order theory for hypersonic speeds is needed the least!