. Response to an Arbitrary Vertical Gust

If the subsonic sharp-edged gust functions are approximated in exponential form, the same techniques used previously to find the total unsteady lift to an arbitrary forcing can be applied. Within the assumptions of the linear theory, a general stationary vertical gust field, wg(x, t), can be decomposed into a series of sharp-edged vertical gusts of small magnitude. When the approximation to the aerodynamic response for sharp-edged vertical gust is found, then the response to an arbitrary vertical gust field can be found using linear superposition by means of Duhamel’s integral. After the initial transient dies out, the response to a continuous vertical gust field may be written analytically as

ЛС*(s) = ^ jf ^-^(s – a, M)da^. (8.191)

As described previously, the Duhamel superposition can be performed numerically in various ways, including the state-space (continuous time) form or the one-step recursive formulation (discrete time) form. In the latter case, a finite-difference approximation to the Duhamel integral leads to a solution for the lift that may be constructed from an accumulating series of small vertical gust inputs using

ACf (0 = j-i [ wg(s) – Z,(,) – Z2(i)] , (8.192)

where the terms Z and Z2 are the deficiency functions. In this case, using Algorithm D-2 given previously in Section 8.14.1, the deficiency functions are given by the one-step recursive formulas

Z(s) = Z(s — As)E + G[lUgC?) — wg(s — As)]#^, (8.193)

Z2CS) = Zt{s — £ss)E2 + G2[u;g(s) — wg(s — A, s)]E2/2, (8.194)

where E1 = exp(—g f2As) and E2 = exp(—g2d2As).

By applying Laplace transforms to the exponential approximation to the sharp-edged vertical gust function in Eq. 8.188, the lift transfer function relating the output (the lift) to the input (the vertical gust field) can be obtained. From the transfer function, the alternative state-space form of the equations can be written as

Ui(Ol_r 0 1 lfzi(Ol

l^(OJ _-glg2{^r)2 P* ~(g + g2) (^) P2 J і Z2(0 I

| 1 0 j AWg(t)

a Lift

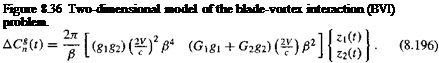with the corresponding output equation for the total normal force (lift) coefficient for the arbitrary vertical gust field as

These equations can then be solved using a standard ordinary differential equation solver for any arbitrarily imposed vertical gust field.