The static stability derivative Mw

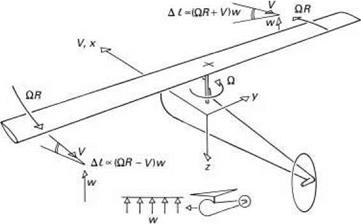
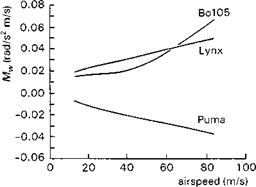
In simple physical terms the derivative Mw represents the change in pitching moment about the aircraft’s centre of mass when the aircraft is subjected to a perturbation in normal velocity w or, effectively, incidence. If the perturbation leads to a positive, pitch-up, moment, then Mw is positive and the aircraft is said to be statically unstable in pitch; if Mw is negative then the aircraft is statically stable. Static stability refers to the initial tendency only and the Mw effect is analogous to the spring in a sim­ple spring/mass/damper dynamic system. In fixed-wing aircraft flight dynamics, the derivative is proportional to the distance between the aircraft’s centre of mass and the overall aerodynamic centre, i. e., the point about which the resultant lift force acts when the incidence is changed. This distance metric, in normalized form referred to as the static margin, does not carry directly across to helicopters, because as the incidence changes, not only does the aerodynamic lift on the rotor change, but it also rotates (as the rotor disc tilts). So, while we can consider an effective stafic margin for helicopters, this is not commonly used because the parameter is very configuration dependent and is also a function of perturbation amplitude. There is another reason why the static mar­gin concept has not been adopted in helicopter flight dynamics. Prior to the deliberate design of fixed-wing aircraft with negative static margins to improve performance, fundamental configuration and layout parameters were defined to achieve a positive static margin. Most helicopters are inherently unstable in pitch and very little can be achieved with layout and configuration parameters to change this, other than through the stabilizing effect of a large tailplane at high-speed (e. g., UH-60). When the rotor is subjected to a positive incidence change in forward flight, the advancing blade expe­riences a greater lift increment than does the retreating blade (see Fig. 2.25). The 90° phase shift in response means that the rotor disc flaps back and cones up and hence applies a positive pitching moment to the aircraft. The rotor contribution to Mw will tend to increase with forward speed; the contributions from the fuselage and horizontal stabilizer will also increase with airspeed but tend to cancel each other, leaving the rotor contribution as the primary contribution. Figure 2.26 illustrates the variation in Mw for the three baseline aircraft in forward flight. The effect of the hingeless rotors on Mw is quite striking, leading to large destabilizing moments at high speed. It is

Fig. 2.25 Incidence perturbation on advancing and retreating blades during encounter with vertical gust

Fig. 2.26 Variation of static stability derivative, Mw, with forward speed for Bo105, Lynx and Puma

interesting to consider the effect of this static instability on the dynamic, or longer term, stability of the aircraft.

A standard approximation to the short-term dynamic response of a fixed-wing aircraft can be derived by considering the coupled pitch/heave motions, assuming that the airspeed is constant. This is a gross approximation for helicopters but can be used to approximate high-speed flight in certain circumstances (Ref. 2.16). Figure 2.27 illustrates generalized longitudinal motion, distinguishing between pitch and incidence. For the present, we postulate that the assumption of constant speed applies, and that the perturbations in heave velocity w, and pitch rate q, can be described by the linearized equations:

Iyyq — 5 M

1/

constant incidence a varying pitch в

constant pitch в varying incidence a

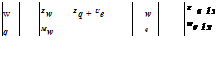where Iyy is the pitch moment of inertia of the helicopter about the reference axes and Ma is the mass. Ue is the trim or equilibrium forward velocity and b Z and b M are the perturbation Z force and pitching moment. Expanding the perturbed force and moment into derivative form, we can write the perturbation equations of motion in matrix form:

The derivatives Zw, Mq, etc., correspond to the linear terms in the expansion of the normal force and pitch moment, as described in eqn 2.45. It is more convenient to discuss these derivatives in semi-normalized form, and we therefore write these in eqn 2.50, and throughout the book, without any distinguishing dressings, as

The solution to eqn 2.50 is given by a combination of transient and steady-state com­ponents, the former having an exponential character, with the exponents, the stability discriminants, as the solutions to the characteristic equation

Л2 — (Zw + Mq)X + Zw Mq — Mw (Zq + Ue) — 0 (2.52)

According to eqn 2.52, when the static stability derivative Mw is zero, then the pitch and heave motions are uncoupled giving two first-order transients (decay rates given by Zw and Mq). As Mw becomes increasingly positive, the aircraft will not experience dynamic instability until the manoeuvre margin, the stiffness term in eqn 2.52, becomes zero. Long before this however, the above approximation breaks down.

One of the chief reasons why this short period approximation has a limited appli­cation range with helicopters is the strong coupling with speed variations, reflected in the speed derivatives, particularly Mu . This speed stability derivative is normally zero for fixed-wing aircraft at subsonic speeds, on account of the moments from all aerody­namic surfaces being proportional to dynamic pressure and hence perturbations tend to cancel one another. For the helicopter, the derivative Mu is significant even in the hover, again caused by differential effects on advancing and retreating blades leading to flapback; so while this positive derivative can be described as statically stable, it
actually contributes to the dynamic instability of the pitch phugoid. This effect will be further explored in Chapter 4, along with the second reason why low-order approxima­tions are less widely applicable for helicopters, namely cross-coupling. Practically all helicopter motions are coupled, but some couplings are more significant than others, in terms of their effect on the direct response on the one hand, and the degree of pilot off-axis compensation required, on the other.

Alongside the fundamentals of flapping, the rotor thrust and torque response to normal velocity changes are key rotor aeromechanics effects that need some attention on this Tour.