TSD equation analysis

The simplest description of transonic flow is provided by the TSD equation (8.59) derived earlier, which can be re-written in the following form.

S фхх + фуу + фХХ — 0 (8.170)

S(r) = 1 – Ml – (y+1)Ml фх ~ 1 – M2 (8.171)

Superficially, the TSD equation has the same form as the PG equation, except the global coefficient 1—Ml is replaced by the local coefficient S(r). This is approximately the local 1 — M2 value, to first order in

the perturbation x velocity фх. The assumption Ml ~ 1 was also made to slightly further simplify the y+1

factor in the higher-order фх term. This S is in effect a “sonic discriminator,” since S > 0 in subsonic regions which have a Laplace-like behavior, and S < 0 in supersonic regions which have a wave-like behavior. The TSD equation in the transonic regime is therefore a PDE of mixed type. The sonic line (or sonic surface in 3D) which forms the boundary of the supersonic zone is the M — 1 or S — 0 isocontour.

It’s useful to see how the nonlinearity of the TSD equation is capable of representing shock waves. To examine this we consider the 2D TSD equation written in divergence form,

(1-Ml )фх

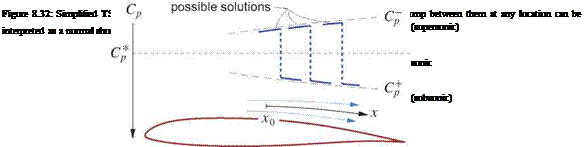and integrate this over a small distance xo…x, as shown in Figure 8.32.

We will assume that фгг ~ A is constant, which corresponds to the streamlines being convergent (A < 0) or divergent (A > 0).

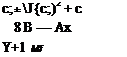The integration constant B will depend on A and also on the value of фх at the initial point x0. The above relation (8.173) is a quadratic equation for the perturbation speed фх, or equivalently Cp — -2фх, which has the following solution.

This admits two distinct solutions, C+ > C* (subsonic) and Cp < C* (supersonic), which can be inter­preted as the flows on the two sides of a normal shock This simplified analysis does not predict where the shock will occur, which in an actual TSD solution would be implicitly determined by the freestream Mach number and the overall airfoil geometry