8.7 THE RESPONSE OF A RIGID AIRPLANE TO ATMOSPHERIC TURBULENCES

As an illustration of the statistical approach, let us consider the motion of an airplane in response to atmospheric turbulences. For simplicity, let us use the assumptions listed in § 8.2 (except 6), that the airplane may be regarded as a rigid body, that the forward velocity U can be regarded as a constant, that the disturbed motion is symmetrical with respect to the longitudinal plane of symmetry, and that the pitching motion can be neglected and only the translational motion normal to the flight path is of significance. Moreover, we shall assume that only the velocity com­ponent of turbulence normal to the flight path need be considered. The effect of other velocity components will be neglected.

The characteristics of atmospheric turbulences may depend on the geographic and weather conditions. However, Clementson8-47 has shown, that the correlation functions (and the power spectra) of atmospheric turbulences, in several different conditions (unstable air mass, water-land discontinuities, thunderstorms, and mountainous terrain), are, aside from a constant multiplier, remarkably similar to each other. They differ essentially only in intensity.

The following analysis will not refer to any particular weather condition but to isotropic turbulences as measured in wind tunnels.

We assume, therefore, that the mean value of the gust fluctuation is zero and that the gust has a power spectrum given by p2{co) of Eq, 26 of § 8.5, which can be written as

where w2 is the mean square intensity of the gust, l is the scale of turbu­lence, and U is the speed of the general flow, i. e., the speed of flight of the airplane. The scale of turbulence is defined by the area under the normalized correlation curve

Let us consider first an airfoil strip of unit span in a two-dimensional flow. Let the mean flow velocity be U which is parallel to the mean posi­tion of the airfoil chord. The airfoil is assumed thin, and the amplitude of its motion is assumed small in comparison with the chord. On the mean velocity of flow U is superposed a small turbulent fluctuation w, uniform across the span, and normal to the chord. The turbulent motion in the fluid may be regarded as transported with the mean flow, so that w is given by a stationary random function

The lift that acts on the airfoil is partly due to the disturbance w and partly due to the motion of the airfoil itself. Within the framework of the linearized theory the lift induced by these two parts are superposable. The equation of motion of the airfoil (having the translational degree of freedom) can be written as

mz – f L(z) = — L(w) (4)

where L(w) indicates the lift induced by w(t), and L(z) that due to the motion of the airfoil. Regarding — L(w) as a known external force, Eq. 4 is the same as Eq. 10 of § 6.8, describing the disturbed motion of an air­foil. Thus it is seen that the problem of the response of an airfoil to a turbulent flow can be separated into two parts:[25] (1) the determination of the lift produced by the turbulent flow on an airfoil in a steady flow, and (2) the determination of the disturbed motion of the airfoil due to an exciting force, with the flow regarded as uniform and without turbulence.

According to the results in § 8.6, if the power spectrum of the turbulence w{t) is jPgUSt(w), that of the lift would be

Pm(°>) = (5)

where xa{w) denotes the square of the absolute value of the frequency response (admittance) of the lift to a sinusoidal gust. The power spectrum of the airfoil acceleration would be

Accfa) = У.1т) УЛт) ^gust(w) (6)

where xs{p) denotes the square of the absolute value of the frequency response of the acceleration to a sinusoidal lift force. Hence, the problem is finally resolved to the determination of the quantities Хз(ы) and Xa(w)- If we introduce the strip assumption that each section of an airfoil can be regarded as a two-dimensional airfoil, neglecting the effect of finite span, then the above argument can be applied to the whole airplane. We shall consider this problem in greater detail below.

Lift Due to a Sinusoidal Gust. Let the coordinate axes be fixed on the airfoil, with the origin x = 0 located at the mid-chord point. Let the vertical gust velocity be given by the expression

w(x, t) = w0 eim{t-xlV) (7)

which shows a sinusoidal gust pattern moving past the airfoil with a speed U. In § 13.4, it will be shoVn that the lift induced by w(x, t) on a two-dimensional airfoil of unit span is

L = 2rrpbUw0 ешф(к) (8)

where p is the air density, b is the semichord length, к is the reduced

frequency соЬ/и, and

* ПГЇ5 <9>

The resultant lift acts through the Vrcliord point from the leading edge. The factor 2прЫ1ф(к) represents the frequency response (admittance) of the lift to the gust.

Admittance of the Airplane. The equation of motion of a two-dimen­sional airfoil subject to a sinusoidal force has been derived in § 6.8. In a single degree of freedom of vertical translation, Eq. 10 of § 6.8 gives

-L(t) + P(t) (10)

where m = the mass of the airfoil

r = a dimensionless time = Utjb z! — dzjdx, г" = dh/di2

/>£%*■ ~2S~b

The lift per unit span on the two-dimensional wing is given by an integral in Eq. 8 of § 6.8. Neglecting the lift on the tail surfaces, and using strip assumption, we can write the lift од the airplane as

where S = wing area, and Ф(т — т0) is the Wagner’s function.

In a simple-harmonic motion

2 = z0eimt = z0eikT, P = Р0еш = P0eikT (11)

the lift can be written as (compare Eqs. 7 and 9 of § 6.9)

L{r) = ^ S j^2C(Ar) j z, – k2 eikT (12)

Hence, the equation of motion is

{- m ~ k* + ^ I [2 am – ^]) z0 = P0 (13)

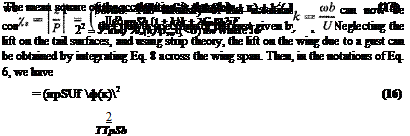The quantity in { } is the complex impedance from P(r) to z(r). Its inverse, multiplied by — со2 == — (Uk/b)2, gives the admittance of the acceleration z. Introducing the airplane density ratio к as a parameter,

The exact integration of the above expression is difficult because of the complicated manner in which the Bessel functions are involved. To obtain an approximate solution, let us note that in the full range (0, oo) G2 is much less than F2. Hence we may neglect terms involving G2 in Eqs. 17. Moreover, since

while in practice, к varies from a number of order 40 for trainers and transports to 150 for high-speed fighters, a fair approximation of Eq. 17 is simply the quasi-steady result

The variation of /(a, s’) is shown in Fig. 8.11. Note that z2 -> 0 both when s -> 0 and when s-*■ oo. Hence, as the scale of turbulence becomes either negligibly small or infinitely large in comparison with the wing chord, the intensity of the acceleration experienced by the airplane will tend to zero. This can be expected, because, when the wing chord is very large in comparison with the turbulence scale, the “gusts” are smoothed out by canceling each other over the wing. On the other hand, when the chord length is very small in comparison with the scale of turbulence, the airfoil behaves quasi-stationarily. A rigid airplane having only the trans­lational degree of freedom will experience no acceleration in a steady flight; hence, the limiting case z2->0ass->0.

The importance of the critical speeds of aeroelastic stability on the dynamic-stress problem is evident from the airplane admittance to the sinusoidal lift. For example, when flutter speed is approached, %s(w) will become very great, thus causing very large dynamic stresses.

The mean square value of the acceleration z is thus known as a function of the airplane speed, mass, and size, and the intensity and scale of the turbulence. From the assumption of stationariness of the gusts, the time averages are equal to the ensemble averages. Hence, z2 is also the standard deviation of an ensemble of gust responses. According to the interpretation given in § 8.4, it gives some idea of the dispersion of the induced acceleration caused by the gusts. The mean value being zero,

and the standard deviation being known, two of the most important para­meters of the probability distribution of the gust response are determined.

In order to compare Eq. 23 with Eq. 10 of § 8.2, we may assume к 1 and reduce Eq. 23 into the form

V£ __ brp^w2US 1I(a, s) g 2 mg ^ n

whence, upon defining (z2)I,2/g as the mean acceleration Дn, and (w2)l,‘ as a mean gust speed w0, and replacing 2n by the lift curve slope dCLjda, we obtain8-44

Comparing this with Eq. 10 of§ 8.2, we see that they are identical but for the factor V/(a, s)/tt, which may be identified with the usual “gust allevia­tion factor.” Williams8-44 points out that, if we use the peak value of the
7(oc, s) curve in (24), a proper account of the effect of airplane mass ratio on gust response is obtained. Moreover, the existence of a peak in the /(oc, s) curve means that an airplane responds more readily to a scale of turbulence which is a constant multiple of wing chord, the constant being dependent upon the mass ratio. This explains a rather interesting experi­mental result that the so-called “gust gradient distance” is more closely related to the wing chord, rather than to the meteorological conditions.

If the probability-distribution function of the gust response is deter­mined, the probability of encountering an acceleration of a specified mag­nitude can be found according to statistical methods. The probable number of times when the dynamic stresses in the structure exceed a specified stress level can be computed. Such information will be useful in designing an aircraft with respect to fatigue and service life. Engin­eering applications of this nature are discussed in Refs. 8.39-8.44, 8.63 and 8.86.

To obtain complete information about the probability distribution of dynamic stresses, higher-order correlation functions would have to be computed (see § 8.5). Such calculations are usually quite involved (see Mazelsky8 83). In practice, however, some idea about the probability distribution can often be obtained by experimental means, and a know­ledge about the mean value and the root-mean-square deviation of the random variable is sufficient for engineering purpose.

The idea of statistical treatment is not new. The first application of statistical theory to dynamics goes back to Lord Rayleigh. It forms the basis of Taylor8-54 and von Karman’s8-51 theory of turbulence. It is also the foundation of the theory of Brownian motion, of noise in electric and acoustical systems, and of certain aspects of astrophysics. The mathe­matical theory of the stationary time series was developed by Wiener and Kintchine. The type of analysis used in this section was first made by Lin.8-82 its application to aeroelastic problems was first pointed out by Liepmann.9,11

The functions we are concerned with are functions of time and depend on chance. Such a function is known as a stochastic process. A sto­chastic process bears the same relation to a definite function that a random variable does to a definite number. Whereas an ensemble for a random variable may be regarded as the results of observation of a random experiment, an ensemble for a stochastic process should be regarded as a large number of experiments carried out under similar conditions, in which each experiment provides a function of time.

The application of the theory of stochastic process to dynamic problems raises many fundamental questions regarding the philosophy of structural design. Its successful application in the fields of engineering seismology,

gust measurement,8-41~8-43 fatigue-life studies, landing-impact loads,870 and rough-water operations of seaplanes,8-74~8-78 etc., may be noted. In many such applications it is not permissible to consider the random process as stationary. Examples of dynamic response analysis involving nonstationary stochastic process can be found in Ref. 8.70 in which the dynamic loads problem in aircraft structures during landing is treated.