Cole’s Slender Body Theory of Newtonian Flow

The Newton-Busemann formulas can be obtained systematically from an asymp­totic hypersonic small disturbance theory following Cole [66], who introduced the following parameters

Y — 1

A = , (density ratio) (12.140)

Y + 1

1

H = , (hypersonic similarity parameter) (12.141)

M02-2

H y + 1 1

N = — = , (Newtonian flow parameter) (12.142)

t y — 1 M^S2

The small parameter A vanishes in the Newtonian limit y ^ 1 and

1 + A 2

Y = = 1 + 2A + 2 A2 + ••• (12.143)

1 — A

The small parameter S is the slope or maximum thickness ratio S = e/c.

For hypersonic small disturbances, the transverse perturbation velocity v is of order S, while the streamwise perturbation velocity u is of order S2. The density

perturbation is of order unity, while the perturbation in pressure is of order S2. These orders can be determined from shock wave relations or from Prandtl-Meyer expansion, provided M0S is not much less than unity.

Let the Newtonian flow parameter N be fixed as A ^ 0 and H ^ 0. The first order approximate equations obtained from the hypersonic small disturbance equations for the pressure, density and the transverse velocity are (a = 0 for two dimensional flow and a = 1 for axial symmetry)

The continuity equation is satisfied automatically. The momentum equation reads

1 дф д p

F" + = 0

Fa дr дr

By integration from the surface r = 0, one obtains

Fa F " ф + p = p0(x )

where ф = 0 at r = 0.

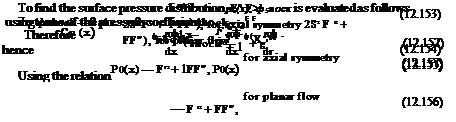
Notice that the surface pressures are independent of the Newtonian parameter N, although the flow field and shock shape depend on N (i. e. the limiting values of the surface pressures as N ^<x> should be a good approximation over a wide range of Mach numbers).

The entropy equation states that p/p — K(ф). From the shock relation K — F’2 + N on the shock, and since rfshock is given before, K (ф) can be found parametrically.

At x — 0, ф — 0 and K(0) — F/2(0) + N, so that

The surface temperature is found from the equation of state, where

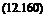p0 — 1 + "02S’2 p — ІЇ

so that the surface temperature is constant

T F /2(0) K (0)

— +1 — + T0 N N

For cones, the first approximation is F (x) = x, 6 = tan вс and the shock is g(x) = Ax. The shock conditions are

p(x, Ax) = 1

p(x, Ax) = 1/(N + 1) (12.161)

v(x, Ax) = A – (N + 1)

The transverse momentum equation yields = 0, hence p = 1, 0 < r < Ax. From the entropy equation and the shock relations, it follows that the density is constant, p = 1/(N + 1).

The transverse component of the velocity can be found from the continuity equa­tion

(12.162)

and, using the boundary condition v = 0 at r = 0

This represents a flow filed whose streamlines are more inclined towards the cone surface as r increases.

The shock angle can be found from the boundary condition for v on the shock