EIGENVECTORS

The eigenvectors corresponding to the above modes are given in the Table 9.2. They are not normalized, being to an arbitrary scale. The first and third columns correspond to w > 0, the second and fourth to 6) < 0.

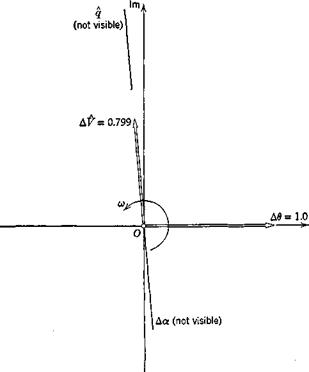
Figure 9.2 is the Argand diagram of the vectors in columns 1 and 3. This is a very effective form of displaying modal characteristics. Since the actual magnitudes of eigenvectors are arbitrary, only the relative lengths of the vectors are shown, taking that of А d = 1.0. The vectors shown can be imagined as rotating and shrinking (just as in Fig. 3.6e except that here we only have those with m positive); and their projections on the Re axis can be thought of as the real values of the indicated variables.

The phugoid is seen to be a motion in which the speed and pitch angle d are the main variables, the former leading the latter by roughly 90° in phase, while the angle of attack and the pitch rate remain virtuafiy constant at their reference values. The flight-path angle Ду is related to Ad and Act by

(5.10,22) , Ay = Ad — Ax, so that in the phugoid Ay = Ad, and the oscilla­tory flight-path angle lags the speed by about 90°.

In the short-period mode, by contrast, there is negligible speed variation, while the angle of attack oscillates with an amplitude and phase not much different from that of Ad. The difference vector Ay is also shown in the figure. This mode as well is one that proceeds essentially in two degrees of freedom, Да and Ad.