Ffowcs Williams-Hawkings Equation

The movement of all the acoustic waves in the field are mathematically embodied in the Ffowcs Williams-Hawkings (FW-H) equation – see Ffowcs Williams & Hawkings

(1969) for the original derivation. This equation incorporates the fundamental principles of
mass, momentum, and energy conservation through a rearrangement of the Navier-Stokes equations in the form of a wave equation – see also Farassat (1975,1981), Brentner (1997a), and Brentner & Farassat (2003). There have been many subsequent studies of the FW-H equation, including reformations of the equations into different forms that are suitable for different forms of analysis and for use with different types of numerical techniques.

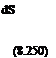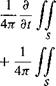According to the FW-H equation the acoustic pressure at a point x at time t can be written in the form

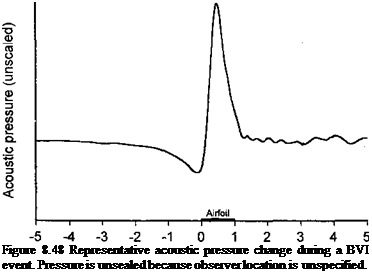
where Zr is the total force on the fluid at each source point on the blade surface S in the direction of the observer and r is the retarded time. The first term in Eq. 8.250 is the thickness noise, which involves a determination of the perturbation velocity, v„, which is produced by the blade as it passes through the flow. The second and third terms are called the loading noise. The third term is a near-field term, which does not represent a propagating wave. Notice that first part of the loading noise is related to the time rate of change of the pressure on the blade. In the compact source limit, this is equivalent to the time rate of change of the lift, which for a BVI event is known to have rapid changes (see previously in Fig. 8.37). As shown in Fig. 8.48, the qualitative nature of BVI sound consists of a highly impulsive change in pressure, and this is fundamentally the source of the “thump-thump” noise so commonly produced by helicopters.

In practice, the evaluation of the FW-H equation is performed numerically in a discretized form, for which for rotor applications several variations are possible. A common computer model for helicopter acoustics is the WOPWOP code developed by Brentner (1986), which uses a retarded time formulation. See also Farassat (1975, 1981) and Farassat & Brentner

Distance traveled in chords

(1987), Brentner (2000), Brentner & Jones (2000), and Brentner & Farassat (2003) for further details on solving numerically the FW-H equation. The computational cost of solving the FW-H equation for helicopter acoustic problems, however, continues to be relatively large and more advanced numerical methods that are more accurate and computationally faster continue to be pursued, including parallel processing – see Long & Brentner (2000). The use of an advanced time instead of a retarded time formulation also allows computational time savings, that is, the time required to propagate the sound into the field (observer) point is calculated directly from the known emission (source) times. While this gives results at unequally spaced observer times, the data can be readily sorted into discrete bins with the same arrival time, as suggested by Fig. 8.45. A typical observer time step must be about 0.5° of rotor azimuth to obtain sufficient temporal resolution. If the observer time overlaps one discrete bin width, then the acoustic information can be weighted over adjacent bins by applying weighting factors. After the complete noise signal is obtained at the observer location from all the sound sources, the time derivative on the appropriate terms in the FW-H equation are taken using a finite-difference formula.