Gated Intensity Ratio Method

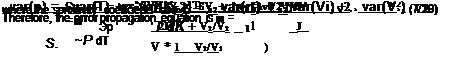
In the gated intensity ratio method for the sinusoidally modulated excitation light, pressure can be expressed as a function of the gated detector output ratio V2 / V1

= Ksv

Ksv P dKsy

S0 = — ^ = 1 + 1/(KsvP) , 0 P дто

P dV2

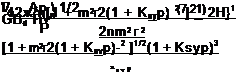In the photon-shot-noise-limited case, the uncertainties in the detector outputs are var(V1) = V1Ghv Bd and var(V2) = V2Ghv Bd. Thus, the photon-shot-noise – limited pressure uncertainty for the gated intensity ratio method is

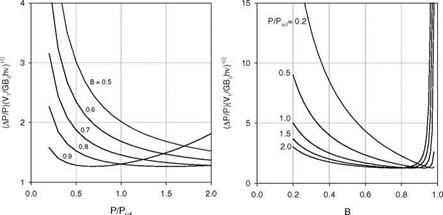
Figure 7.19(a) shows the normalized pressure uncertainty (Ap/pXV1 /GhvBd )1/2 as a function of p/pref at different values of the Stern-Volmer coefficient B for at0 = 10 and H = 1. Figure 7.19(b) shows the normalized pressure uncertainty (Ap/pXVmean/GhvBd )1/2 as a function of B at different values of p/pref for at0 = 10 and H = 1. Similar to the amplitude demodulation method, there is an optimal value of B (around 0.8) to achieve the minimal value of (Ap/pXVmean/GhvBd )1/2. In general, to reduce the noise, the gated intensity ratio method has to collect sufficient photons over a large number of cycles. For

example, compared to a standard CCD camera system with an integration time of 1 second, a gated CCD camera with a modulation frequency of 50 kHz needs to accumulate photons over 100,000 cycles to achieve the equivalently small uncertainty. The accumulation of photons can be done automatically in a phase sensitive camera.

(a)

Fig. 7.19. The normalized pressure uncertainty (Ap/pXVj /Ghv Bd )1/2 for the gated intensity method using a sinusoid modulation with mx0 = 10 and H = 1 as a function of P/Pref for different values of the Stern-Volmer coefficient B, and a function of B for different values of p/pref

SV ) + S 2 var( Tq) + S 2 var(V1) + S2 var(V2)
T
2	2	V22 (7.23)
k2	V12
0
k*

= , KSV P dKSF ’ s „ =- Iе = і+i/(Ksvp),

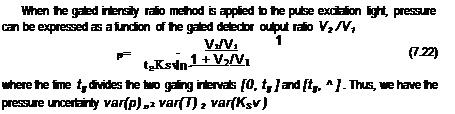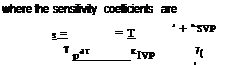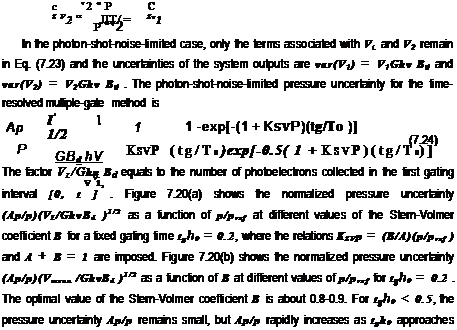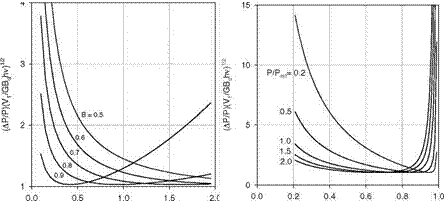
(a) (b) Fig. 7.20. The normalized pressure uncertainty (Ap/p)(V1/GhvBd )1/2 for the gated intensity method with a pulse excitation and tg/x0 = 0.2 as (a) a function of p/pref for different values of the Stern-Volmer coefficient B, and (b) a function of B for different values of p/pref