Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Lift and Induced Drag
 |
 |
 |
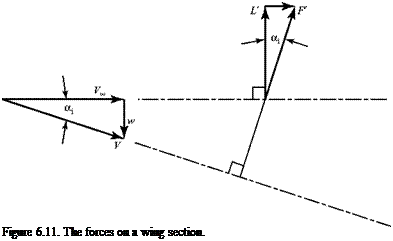
The effect of the presence of downwash also must be examined from the viewpoint of the forces on a wing section. Consider Fig. 6.11. The Kutta-Joukouski Theorem states that the force generated by flow over a bound vortex per unit span is given by F’= pFT and is normal to V—that is, normal to the relative wind. (In two dimensions, the relative wind is the freestream and the force perpendicular to this wind is then the lift force.) It follows from Fig. 6.11 that:
or, finally
L = pV^T.
 |
This is identical to the two-dimensional result.
Notice, now, in Fig. 6.11 that the effect of the downwash is to tilt back the force vector, F ‘, at the lifting line; it is no longer perpendicular to the freestream direction as it was in the two-dimensional case. There is now a component of F’ in the freestream direction that, by definition, is a drag force. This drag force is called the induced drag because it arises due to the presence of the downwash, which is caused by the velocity induced by the trailing-vortex sheet. The induced drag per unit span is given the symbol D. Then, because a is small (see Example 6.3):
Dj = L’ tan aj = L’Oj. (6.18)
The induced drag is an important new concept. It was not present in two-dimensional airfoil theory because there was no trailing-vortex sheet present in that theory. Induced drag arises in inviscid finite-wing theory. It is the price for generating lift with a three-dimensional wing. Induced drag may be thought of physically as representing energy left behind an advancing wing. This energy is in the form of translational and rotational kinetic energy present in the trailing vortices. These vortices are deposited in the atmosphere and, ultimately, are dissipated by viscosity.
Induced drag is a significant drag contribution. Although aj is small, in Eq. 6.18, it multiplies the lift per unit span, which is a large number proportional to the weight of the flight vehicle. Thus, induced drag must be studied and methods sought to minimize the magnitude of this drag. Recall from Chapter 1 that flight-vehicle performance and efficiency are directly dependent on making the drag from all sources as small as possible.
