ROBUST STABILITY

Robust stability is first analyzed with the ц tool (see Figure 9.1). The maximal value of the mixed fi upper bound is 0.24 at ui = 228 rad/s, so that the maximal uncertainty in the stability derivatives is 5/0.24 « 20%. However, in the context of (Balas and Packard, 1992), the controller must tolerate a given amount of uncertainty in the bending mode, as defined

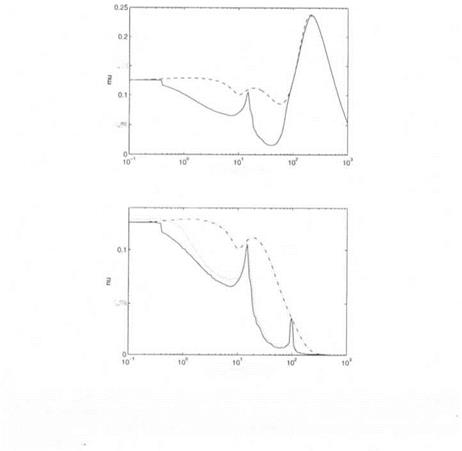by the template. It is thus logical to maintain this uncertainty inside its unit ball in the analysis problem. The maximal value of the first mixed v upper bound is obtained as 0.13 at ш = 0.1 rad/s, so that the maximal uncertainty in the stability derivatives becomes 5/0.13 « 40% (see Figure 9.1).

D 15

frequency m rad’s

frequency in rad/s

Remarks:

(i) In figures 9.1 to 9.3, "mixed fj, upper bound" should be understood as the /л upper bound by (Fan et al., 1991), whereas the ‘mixed // lower bound" should be understood as the ц lower bound by (Young and Doyle, 1990). The "complex /x upper bound" corresponds to the specialization of the mixed ц upper bound to the case of complex uncertainties (see subsection 2.2 of chapter 5 – in the context of the missile example, the real nature of the parametric uncertainties is not accounted for in the

computation of the complex /r upper bound). The "first mixed и up­per bound", the "second mixed у upper bound" and the "mixed ^ lower bound" are defined in chapter 8.

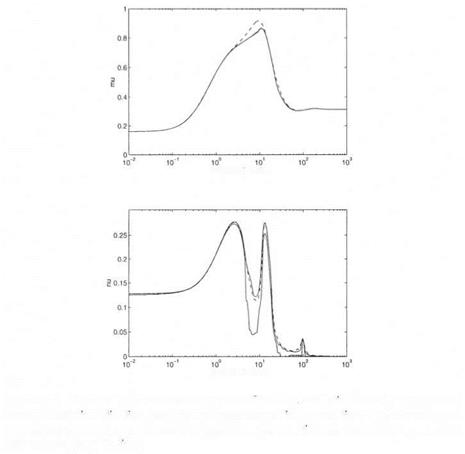(ii) Neither the mixed p lower bound, nor its skewed version are presen­ted in Figure 9.1, since the power algorithms did not converge. The p problem at low and medium frequencies is indeed too close to a real p problem.