Some Basic Observations

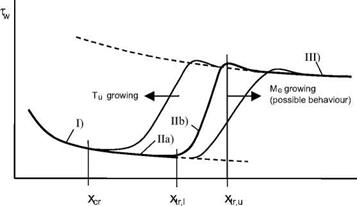
We consider laminar-turbulent transition of the two-dimensional boundary layer over a flat plate as prototype of regular transition, and ask what can be observed macroscopically at the plate’s surface. We study the qualitative behavior of wall shear stress along the surface, Fig. 8.1.[120] We distinguish three branches of tw. The laminar branch (I) is sketched in accordance with tw ж x-0’5, and the turbulent branch (III) with tw ж x-0’2, Table 7.5. We call the distance between xcr and xtr, u the transitional branch (II). In consists of the instability sub-branch (IIa) between xcr and xtr, i, and the transition sub-branch (IIb) between xtr>l and xtr, u. The instability sub-branch overlaps with the laminar branch (see below).

In Fig. 8.1 xcr denotes the point of primary instability (critical point). Upstream of xcr the laminar boundary layer is stable, i. e., a small distur­bance introduced into it will be damped out. At xcr the boundary layer is

neutrally stable, and downstream of it is unstable. Disturbances there trigger Tollmien-Schlichting waves (normal modes of the boundary layer) whose am­plitudes grow rather slowly.[121] Secondary instability sets in after the Tollmien – Schlichting amplitudes have reached approximately 1 per cent of ue, i. e., at amplitudes where non-linear effects are still rather small regarding the (pri­mary) Tollmien-Schlichting waves. Finally turbulent spots appear and the net-production of turbulence begins (begin of sub-branch IIb). This location is the “lower” location of transition, xtr, i. At the “upper” location of transi­tion, xtr, u, the boundary layer is fully turbulent.[122] This means that now the turbulent fluctuations transport fluid and momentum towards the surface such that the full time-averaged velocity profile shown in Fig. 7.5 b) develops. The picture in reality appears not to be that simple [19]. It seems that this location still lies in the intermittence region Ax’tr (see below), where the intermittency factor is approximately 0.5.

The length of the transition region, related to the location of primary instability, can be defined either as:

Axtr xtr, l xcr 1 (8.1)

or as

Axtr — xtr, u xcr • (8.2)

One has to bear this in mind when using empirical and semi-empirical stability/transition criteria, Sub-Section 8.4.2.

In Fig. 8.1 some important features of the transition region are indicated:

— In the instability sub-branch (Ila) between xcr and xtr>l the time-averaged (“mean”) flow properties practically do not deviate from those of laminar flow (branch I). This basic feature permits the formulation of stability and in particular transition criteria and models based on the properties of the laminar flow branch. This is of very large importance for practical instability and transition predictions, the latter still based on empirical or semi-empirical models and criteria.

— The transition sub-branch (IIb) (intermittency region), i. e., Ax’tr — xtr, u — xtr, i, usually is very narrow.[123] It is characterized by the departure of tw from that of the laminar branch and by its joining with that of branch III. For boundary-layer edge flow Mach numbers Me A 4 to 5 the (tempo­ral) amplification rates of disturbances can decrease with increasing Mach number, therefore a growth of Ax’tr is possible. In such cases transition criteria based on the properties of the laminar flow branch would become questionable. The picture in reality, however, is very complicated, as was shown first by Mack in 1965 [18, 21]. We will come back to that later.

— At the end of the transitional branch (II), xtr, u, the wall shear stress over­shoots shortly that of the turbulent branch (III).[124] This overshoot occurs also for the heat flux in the gas at the wall. At a radiation-adiabatic sur­face this overshoot can lead to a hot-spot situation relative to the nominal branch III situation.

— With increasing disturbance level, for example increasing free-stream tur­bulence Tu in a ground-simulation facility, the transition sub-branch (IIa) will move upstream while becoming less narrow, see, e. g., [22]. When dis­turbances grow excessively and transition becomes forced transition, tran­sition criteria based on the properties of the laminar flow branch (I) become questionable in this case, too.

— In general it can be observed, that boundary-layer mean flow properties, which destabilize the boundary layer, see Sub-Section 8.1.3, shorten the length of sub-branch IIa (xtr, i — xcr) as well as that of sub-branch IIb (xtr, u — xtr l). The influence of an adverse stream-wise pressure gradient is most pronounced in this regard. If the mean flow properties have a stabilizing effect, the transition sub-branches IIa and IIb become longer.