Spanwise-Lift Distribution on an Arbitrary Wing by Lifting-Line Theory
When faced with solving an integro-differential equation to find the chordwise- vorticity distribution in two-dimensional airfoil theory (see Chapter 5), a Fourier – series representation for the chordwise vortex-strength distribution, y(x), is used. Here, a Fourier series is used to represent the unknown bound-vortex-strength distribution, Г(у), in Eq. 6.21. As in Chapter 5, a transformation is made to relate a span – wise linear location to a location described by angular measure. For example, a circle of radius b/2 with the center at mid-span and measuring the angle 0 from the positive у axis (Fig. 6.14). The required transformation is:
b
b/2 7
Now, we assume a Fourier-series representation of the bound-vortex-strength distribution as given by:
Г(0) = {WVJ^An sinnG, (6.23)
n=1
where An are unknown constants. Because L’ (hence, Г) must be zero at the wing tips by physical argument, there is no lead constant term in the series. For symmetrical spanwise loading, all of the cosine terms vanish because they never make a symmetrical contribution about the wing plane of symmetry, y = 0 or 0 = n/2 and because the cosine is positive for 0 < 0 < n/2 and negative for n/2 < 0 < n. The coefficient (2b VJ is introduced for convenience from hindsight. Equation 6.23 is a solution only if a method for finding the An’s can be established.
We examine the integral term in the defining equation, Eq. 6.21 and call it I. Writing:
dr = dr d0
dy d0 dy ’
|
1 bb2 (dr/dy) 4nV~-b/2 (Ус"У) |
the integral term becomes, with the aid of Eq. 6.22:
Using Eq. 6.23 to find dr/d0 in the integrand and inverting the limits of integration, this expression for I may be written as:
1 ~ П cos n0
– n=1 (cos 0- s 0)d0. (6.24)
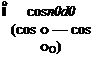 |
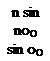 |
As in two-dimensional thin-airfoil theory, this integrand has a singularity when the running variable of integration, 0, is equal to the fixed angle 0O, which denotes the spanwise station of interest. The “principle value” of this integral is used here as in Section 5.14, Eq. 5.57; namely:
Then, the integral in Eq. 6.24 becomes
Finally, we substitute this expression for the integral in the defining equation, Eq. 6.21, and drop the subscript “0” because the equation must hold at any general spanwise station:
4b ^ – sin n0
a(0)=0. (6.27)
0 n=1 n=1
This is the equation for determining the Fourier-series coefficients, An. The coefficients are found by applying Eq. 6.29 at several spanwise stations specified by different values of 0 (see Example 6.2). At each station, c, a, and aL0 are known. Thus, a set of simultaneous equations is generated, which can be solved for the unknown An’s. The more terms that are taken in the series (i. e., the more spanwise stations at which Eq. 6.27 is applied), the more accurate are the coefficients and the theoretical results. With the An’s known, the spanwise loading follows from Eq. 6.23.
If the spanwise loading is symmetrical, then Г(0) = Г(-0). That is, symmetry demands that:
^ Ansm n0 Ansm n(n-0).
n=1 n=1
Expanding the right side of this equality:
N N
^ An sm n0 = ^ An [sin nn cos n0 – cos nn sin n0).
n=1 n=1
Now, sin nn is zero for all integers n, but cos nn = -1 only for n odd. So, if the identity is to be satisfied, there can be no terms appearing with n even. This means that for symmetrical loading the An’s must be zero for all even values ofn. Likewise, for symmetrical loading, we need only calculate the spanwise loading for one semi-span. The loading on the other semi-span is simply a mirror image in the plane of symmetry.
Example 6.2 Given: A wing planform is shown here. This wing has a constant section with a section lift-curve slope of m0 = 6.7 per radian and an angle of zero lift of -1.5°. The wing is symmetrical about y = 0. The wing has geometric twist, with a geometric angle of attack of 4° at the wing root, decreasing linearly with semi-span to 2° at the tips.
Required: Calculate the spanwise loading on this wing. For convenience, calculate only two terms in the Fourier-series expression for r(y). Evaluate the coefficients of these terms at mid-span and at half-semi-span.
Approach: Write two simultaneous equations for the two unknown Fourier-series coefficients. Because the wing is symmetrical, all of the even An’s are zero. The two simultaneous equations for A1 and A3 are obtained by writing Eq. 6.23 twice, once at the spanwise location at y = b/4 (0 = п/3) and once at mid-span (0 = п/2).
Solution: Here, the angle of zero lift is a constant across the span. Because the geometric angle of attack varies linearly, we write the following from the given:
Regarding the chord, from the given geometry of the planform, it is 10 ft. at the root and 7.5 ft. at mid-semi-span. Then, writing Eq. 6.23 at mid-span,
y = 0, 0 = п/2, c = 10:
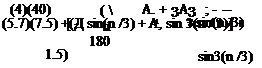 |
|
Again, at mid-semi-span, y = b/4, 0 = п/3, c = 7.5:
solving for the two unknowns, A1 = 0.018 and A3 = -0.0047.
Thus, to two terms:
Г = 2(40)R4(0.018)sin 0 – (0.0047) sin 30]
from Eq. (6.25).
Appraisal: The angles that appear in the defining equation must be expressed in radians. The resulting expression for Г(0) can be expressed as r(y) through the transformation, Eq. 6.24, and evaluated at several values of y, giving the spanwise loading L’ across the span using Eq. 6.18. The loading is symmetrical about y = 0. The number of stations at which the loading is evaluated is independent of the number of stations used to calculate the An’s. However, the more spanwise stations at which the fundamental equation is applied, the more simultaneous equations are generated, and the more accurate is the Fourier series representation for r(y). In the previous example, if a third station was used to generate a third simultaneous equation, the coefficient A5 would be introduced and the values of A1 and A3 would change. The sensitivity of the values of An to the number of simultaneous equations used may be studied by running Program PRANDTL, which is introduced shortly. In this program, the user selects the number of Fourier-series coefficients desired and the computer program solves the simultaneous equation set.
A method for determining the spanwise-lift distribution on a wing of arbitrary planform is now established. Fig. 6.13 shows a calculated spanwise loading, Г(у), for an untwisted tapered wing of constant section at a fixed geometric angle of attack. The loading is nondimensionalized by the value of the circulation at mid-span (У = 0), Г= Го.
Recalling the results in two-dimensional airfoil theory, we might suspect that an integration to find the total forces on the wing would result in a dependence on only a few of the Fourier-series coefficients. This is investigated next.











