Supersonic Flow About Thin Wings

Equation 5.67 is given for the three dimensional velocity potential of a finite wing in a supersonic flow. Let us use this expression and the experiences we have had in handling the two dimensional supersonic flow to obtain the downwash expression.

For this purpose we take the derivative of the integral expression 5.67 with respect to z using Leibnitz rule.

The derivative of the first term of 5.80 reads as

0 Z „0A(n, g)

А(П y + g0 cos O) = — cos O 0Z g0 0g

The second term is given by Eq. 5.70. For the multipliers of the third term we take П = П1, t1 = t2 to obtain

=Tb; A(n У + gocos h)n=n1 = A(n1; y);

(eixT1 + eixT2 )£= n = 2eix(t^iai)

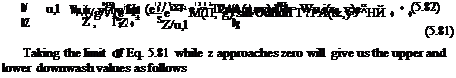The third term now becomes enterable, and we finally have for the downwash

In Eq. 5.67, the unknown source strength was A(x, y). If we use the downwash expression, 5.82, in Eq. 5.67 we obtain an integral expression for the unknown potential in terms of the boundary condition

n1 p

/u, i(x, y, Z, t) = T2pb wи, і(П, y + go cos O) (e‘“T1 + e‘“T2)dn dO (5.83)

00

The exponents of 5.83 can be written Cartesian coordinates to give the fol­lowing expression for the potential

_ і П }2 e-ix^{x-n) cos Щ

фи,1(Х; У Z)=T – g) R – dn dg (5-84)

0 g1

If you use the same nondimensional variables used for the two dimensional case, the amplitude of the velocity potential reads as

We know the relation between the lifting pressure and the velocity potential. Using that relation we obtain

(x‘;y,) = –(<k + о0*) //" fl/°S<~>dn‘ dg* (5.86)

V

Here, the area integral V is the intersection between the wing surface and the upstream Mach cone, and R reads as

R* = /(x*- П*)2-Ь2(у*- П*)2.

In this section, we have obtained the analytical relation for the lifting pressure coefficient as Eq. 5.86. We observe that for two and three dimensional supersonic flows the lifting pressure coefficient can be explicitly obtained from the downwash given at the surface as the boundary condition. This implies, unlike for the case of subsonic flows, determination of the surface pressure discontinuity does not require calculated inversion of an integral equation. Instead, the lifting pressure is computed with direct integration of 5.79 and 5.86.

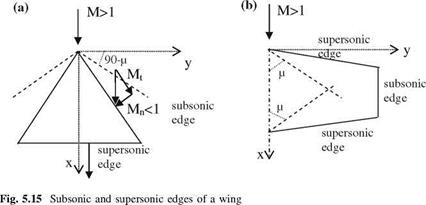
There are two different approaches in calculating the aerodynamic coefficients. The first method uses the analytical approach to calculate these coefficients for special geometries like delta wings. This method is good for rigid body motions like translation and rotation of wings (Miles 1959). The second approach is applicable to wider range of problems and they are approximate numerical methods. There are two different types of numerical methods. The first method is called ‘The Supersonic Kernel Function Method’, and the second one is the ‘Mach Box Method’. Before studying these methods in detail, we have to classify the wing edges as subsonic or supersonic edges. The criteria to decide about the type of the edge depend on the relation between the sweep angle and the Mach angle as indicated in Fig. 5.15.

In Fig. 5.15-a for the delta wing lying in the Mach cone of the flow, the component of the Mach number normal to the leading edge is less than 1,

therefore, the leading edge shown is subsonic. On the other hand, the normal component of the Mach number at the trailing edge is greater than 1, therefore the trailing edge is supersonic. In Fig. 5.15b, only subsonic edge is the tip because the normal component of the Mach number is zero, whereas the leading and the trailing edges are outside of Mach cone and this makes those edges supersonic.